
 如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线所示),则原始的最大流量与当前最大流量的比值为1.2.
如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线所示),则原始的最大流量与当前最大流量的比值为1.2. 分析 建立直角坐标系,求出抛物线方程,然后利用定积分求出泥沙沉积的横截面面积,求出梯形面积,即可推出结果.
解答  解:如图:建立平面直角坐标系,设抛物线方程为:y=ax2,因为抛物线经过(5,2),可得a=$\frac{2}{25}$,
解:如图:建立平面直角坐标系,设抛物线方程为:y=ax2,因为抛物线经过(5,2),可得a=$\frac{2}{25}$,
所以抛物线方程:y=$\frac{2}{25}{x}^{2}$,
横截面为等腰梯形的水渠,泥沙沉积的横截面的面积为:
2×$({∫}_{0}^{5}\frac{2}{25}{x}^{2}-\frac{1}{2}×2×2)$=2($\frac{2}{75}{{x}^{3}|}_{0}^{5}-2$)=$\frac{8}{3}$,
等腰梯形的面积为:$\frac{10+6}{2}×2$=16,当前最大流量的横截面的面积16-$\frac{8}{3}$,
原始的最大流量与当前最大流量的比值为:$\frac{16}{16-\frac{8}{3}}$=1.2.
故答案为:1.2.
点评 本题考查抛物线的求法,定积分的应用,考查分析问题解决问题的能力,合理建系是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
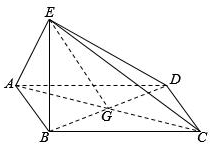 如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
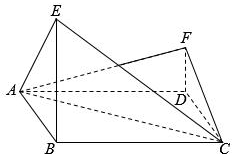 如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面 ABCD,BE=2DF,AE丄EC.
如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面 ABCD,BE=2DF,AE丄EC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0)∪(0,1) | B. | (-∞,-1)∪(1,+∞) | C. | (-$\sqrt{2}$,0)∪(0,$\sqrt{2}$) | D. | (-∞,-$\sqrt{2}$)∪($\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 乘客 | P1 | P2 | P3 | P4 | P5 |
| 座位号 | 3 | 2 | 1 | 4 | 5 |
| 3 | 2 | 4 | 5 | 1 | |
| 3 | 2 | 4 | 1 | 5 | |
| 3 | 2 | 5 | 4 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com