
| A. | $\frac{8}{9}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{3}$ |
分析 根据题意得出a•b>0,列出符合题意的事件即可,求解随机变量的概率,利用数学期望求解即.
解答 解:∵抛物线y=ax2+bx+c(a≠0)的对称轴在y轴的左侧,
∴$-\frac{b}{2a}$<0,
即a•b>0,
∵a、b、c∈{-3,-2,-1,0,1,2,3},
∴可得出:(a,b)的基本事件为:
(-3,-3)(-3,-2)(-3,-1)
(-2,-3)(-2,-2)(-2,-1)
(-1,-3)(-1,-2)(-1,-1)
(1,1)(1,2)(1.3)
(2,1)(2,2)(2.3)
(3,1)(3,2)(3.3)
共18个基本事件,
∵在这些抛物线中,记随机变量X=|a-b|,
∴可得出X=0,1,2,
P(X=0)=$\frac{6}{18}$=$\frac{1}{3}$
P(X=1)=$\frac{8}{18}$=$\frac{4}{9}$.
P(X=2)=$\frac{4}{18}$=$\frac{2}{9}$
∴分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{1}{3}$ | $\frac{4}{9}$ | $\frac{2}{9}$ |
点评 本题考查离散型随机变量的分布列的期望的求法,准确判断随机变量的取值,求出概率是解题的关键,判断a,b符合的条件.


科目:高中数学 来源: 题型:填空题
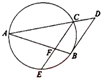 如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D.过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=4,FB=1,EF=2,则线段AC的长为4.
如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D.过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=4,FB=1,EF=2,则线段AC的长为4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cosA=cosB | B. | sinA=sinB | C. | bcosA=acosB | D. | acosA=bcosB |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com