
 已知三棱锥O-ABC,点M,N分别为AB,OC的中点,且$\overrightarrow{OA}$=$\vec a$,$\overrightarrow{OB}$=$\vec b$,$\overrightarrow{OC}$=$\vec c$,用$\vec a$,$\vec b$,$\vec c$表示$\overrightarrow{MN}$,则$\overrightarrow{MN}$等于( )
已知三棱锥O-ABC,点M,N分别为AB,OC的中点,且$\overrightarrow{OA}$=$\vec a$,$\overrightarrow{OB}$=$\vec b$,$\overrightarrow{OC}$=$\vec c$,用$\vec a$,$\vec b$,$\vec c$表示$\overrightarrow{MN}$,则$\overrightarrow{MN}$等于( )| A. | $\frac{1}{2}(\vec b+\vec c-\vec a)$ | B. | $\frac{1}{2}(\vec a+\vec b-\vec c)$) | C. | $\frac{1}{2}(\vec a-\vec b+\vec c)$ | D. | $\frac{1}{2}(\vec c-\vec a-\vec b)$ |
分析 根据所给的图形,在图形中看出要求的向量可以怎么得到,用减法把向量先变化成已知向量的差的形式,再利用向量的加法法则,得到结果.
解答 解:由题意知$\overrightarrow{MN}$=$\overrightarrow{ON}$-$\overrightarrow{OM}$=$\frac{1}{2}$$\overrightarrow{OC}$-$\frac{1}{2}$($\overrightarrow{OA}$+$\overrightarrow{OB}$)
∵$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,
∴$\overrightarrow{MN}$=$\frac{1}{2}$($\overrightarrow{c}$-$\overrightarrow{b}$-$\overrightarrow{a}$)
故选:D.
点评 本题考查空间向量的加减法,本题解题的关键是在已知图形中尽量的应用几何体的已知棱表示要求的结果,本题是一个基础题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:填空题
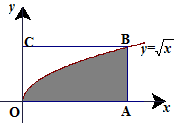 如图,长方形的四个顶点为O(0,2),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B.现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是$\frac{2}{3}$.
如图,长方形的四个顶点为O(0,2),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B.现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是$\frac{2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 264 | B. | 72 | C. | 266 | D. | 274 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
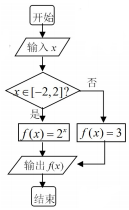
| A. | (-∞,0) | B. | [-1,0] | C. | [1,+∞) | D. | [0,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com