
| A. | 264 | B. | 72 | C. | 266 | D. | 274 |
分析 先安排上午的测试方法,有A44种,再安排下午的测试方式,由于上午的测试结果对下午有影响,故需要选定一位同学进行分类讨论,得出下午的测试种数,再利用分步原理计算出结果.
解答 解:先安排4位同学参加上午的“身高与体重”、“立定跳远”、“肺活量”、“台阶”测试,共有A44种不同安排方式;接下来安排下午的“身高与体重”、“立定跳远”、“肺活量”、“握力”测试,假设A、B、C同学上午分别安排的是“身高与体重”、“立定跳远”、“肺活量”测试,若D同学选择“握力”测试,安排A、B、C同学分别交叉测试,有2种;若D同学选择“身高与体重”、“立定跳远”、“肺活量”测试中的1种,有A31种方式,安排A、B、C同学进行测试有3种;根据计数原理共有安排方式的种数为A44(2+A31×3)=264,
故选A.
点评 本题主要考查了排列与组合的相关知识点,突出对分类讨论思想和数学思维能力的考查,属较难题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 10 | C. | 8 | D. | 2+log35 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知三棱锥O-ABC,点M,N分别为AB,OC的中点,且$\overrightarrow{OA}$=$\vec a$,$\overrightarrow{OB}$=$\vec b$,$\overrightarrow{OC}$=$\vec c$,用$\vec a$,$\vec b$,$\vec c$表示$\overrightarrow{MN}$,则$\overrightarrow{MN}$等于( )
已知三棱锥O-ABC,点M,N分别为AB,OC的中点,且$\overrightarrow{OA}$=$\vec a$,$\overrightarrow{OB}$=$\vec b$,$\overrightarrow{OC}$=$\vec c$,用$\vec a$,$\vec b$,$\vec c$表示$\overrightarrow{MN}$,则$\overrightarrow{MN}$等于( )| A. | $\frac{1}{2}(\vec b+\vec c-\vec a)$ | B. | $\frac{1}{2}(\vec a+\vec b-\vec c)$) | C. | $\frac{1}{2}(\vec a-\vec b+\vec c)$ | D. | $\frac{1}{2}(\vec c-\vec a-\vec b)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-8] | B. | [2,+∞) | C. | (-∞,-8]∪[2,+∞) | D. | (-∞,-8)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3,6,7} | B. | {2,4,6} | C. | {1,3,7,8} | D. | {1,3,6,8} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 29 000元 | B. | 31 000元 | C. | 38 000元 | D. | 45 000元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
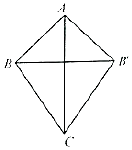 如图所示,在四边形ABCB'中,△ABC≌△AB'C,AB⊥AB',cos∠BCB'=$\frac{3}{4}$,BC=2$\sqrt{7}$,则△BCB'外接圆的面积为8π.
如图所示,在四边形ABCB'中,△ABC≌△AB'C,AB⊥AB',cos∠BCB'=$\frac{3}{4}$,BC=2$\sqrt{7}$,则△BCB'外接圆的面积为8π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com