练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．已知点A（2，0）B（0，-4）
    （1）写出△AOB的外接圆方程
    （2）设直线l：3x-4y-1=0与△AOB的外接圆交于A，B两点，求|AB|

    分析 （1）求出圆心与半径，即可写出△AOB的外接圆方程
    （2）求出圆心到直线l：3x-4y-1=0的距离，利用勾股定理求|AB|．

    解答 解：（1）由题意，圆心坐标为（1，-2），圆的半径为$\sqrt{5}$，
    ∴△AOB的外接圆方程为（x-1）2+（y+2）2=5；
    （2）圆心到直线l：3x-4y-1=0的距离d=$\frac{|3+8-1|}{\sqrt{9+16}}$=2，
    ∴|AB|=2$\sqrt{5-4}$=2．

    点评 本题考查圆的方程，考查直线与圆的位置关系，考查弦长公式，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    1．数列{an}的通项是关于x的不等式x2-x＜nx（n∈N•）的解集中的整数的个数，且已知f（n）=$\frac{1}{{a}_{n}+1}$+$\frac{1}{{a}_{n}+2}$+…+$\frac{1}{{a}_{n}+n}$．
    （1）求数列{an}的通项公式；
    （2）若bn=$\frac{{a}_{n}}{{2}^{n}}$，求{bn}的前n项和Sn；
    （3）求证：对n≥2且n∈N•，恒有$\frac{7}{12}$≤f（n）＜1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知矩阵M=$[\begin{array}{l}{3}&{6}\\{2}&{2}\end{array}]$，则M的特征值为-1或6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．如图，在正方形SG1G2G3中，E，F分别是G1G2，G2G3的中点，D是EF的中点，现沿SE，SF及EF把这个正方形折成一个几何体，使G1，G2，G3三点重合于点G，这样，下列五个结论：（1）SG⊥平面EFG；（2）SD⊥平面EFG；（3）GF⊥平面SEF；（4）EF⊥平面GSD；（5）GD⊥平面SEF．正确的是（　　）
    A．（1）和（3）B．（2）和（5）C．（1）和（4）D．（2）和（4）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

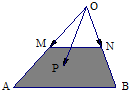    6．如图所示，在△OAB中，M、N分别是OA、OB的中点，点P在梯形ABNM区域（含边界）上移动，且$\overrightarrow{OP}=x\overrightarrow{OM}+y\overrightarrow{ON}$，则4x+3y的取值范围是[3，8]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．若正数a，b满足ab-（a+b）=1，则a+b的最小值是（　　）
    A．2+2$\sqrt{2}$B．2$\sqrt{2}$-2C．$\sqrt{5}$+2D．$\sqrt{5}$-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．求函数f（x）=x3-3x2-9x+2的单调区间和极值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

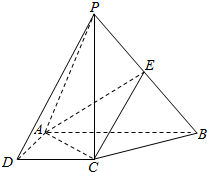    20．如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，AB⊥AD，AB∥CD，AB=2AD=2CD=2，BC=$\sqrt{2}$，且PC⊥CD，BC⊥PA，E是PB的中点．
    （1）求证：平面PBC⊥平面EAC；
    （2）若二面角P-AC-E的正弦值为$\frac{{\sqrt{3}}}{3}$，求直线PA与平面EAC所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．若直线l：y=k（x+1）与圆C：（x-1）2+y2=1恒有公共点，则k的取值范围是$-\frac{{\sqrt{3}}}{3}≤k≤\frac{{\sqrt{3}}}{3}$，，直线l的倾斜角的取值范围是$θ∈[{0，\frac{π}{6}}]∪[{\frac{5π}{6}，π}）$．

    查看答案和解析>>

    同步练习册答案