
分析 由$\overrightarrow{OP}$=$\overrightarrow{OA}$+λ($\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|cosB}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|cosC}$),得$\overrightarrow{AP}$=λ($\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|cosB}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|cosC}$),两边同乘以向量$\overrightarrow{BC}$,利用向量的数量积运算可求得$\overrightarrow{AP}•\overrightarrow{BC}$=0,从而得到结论.
解答 解:由$\overrightarrow{OP}$=$\overrightarrow{OA}$+λ($\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|cosB}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|cosC}$),得$\overrightarrow{AP}$=λ($\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|cosB}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|cosC}$),
两边同乘以向量$\overrightarrow{BC}$,得$\overrightarrow{AP}•\overrightarrow{BC}$=λ($\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|cosB}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|cosC}$)$•\overrightarrow{BC}$=λ($\frac{\overrightarrow{AB}•\overrightarrow{BC}}{|\overrightarrow{AB}|cosB}$+$\frac{\overrightarrow{AC}•\overrightarrow{BC}}{|\overrightarrow{AC}|cosC}$)
=λ($\frac{|\overrightarrow{AB}||\overrightarrow{BC}|cos(-B)}{|\overrightarrow{AB}|cosB}$+$\frac{|\overrightarrow{AC}||\overrightarrow{BC}|cosC}{|\overrightarrow{AC}|cosC}$)=λ(-$|\overrightarrow{BC}|+|\overrightarrow{BC}|$)=0.
∴$\overrightarrow{AP}$⊥$\overrightarrow{BC}$,即点P在在BC边的高线上,
∴P的轨迹过△ABC的垂心.
故答案为:垂.
点评 本题考查平面向量数量积的运算、向量的线性运算性质及其几何意义,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
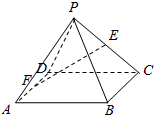 如图,四棱锥P-ABCD中,ABCD为矩形,面PDC⊥面ABCD,∠DPC=90°,E,F 分别为PC,AD的中点.
如图,四棱锥P-ABCD中,ABCD为矩形,面PDC⊥面ABCD,∠DPC=90°,E,F 分别为PC,AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 产品数量x | 0 | 3 | 4 | 6 | 7.2 | 10 |
| 生产成本y | 50 | 72.5 | 82 | 104 | 119.2 | 160 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{3}{2}$,$\frac{3}{2}$) | B. | (-$\frac{9}{4}$,$\frac{9}{4}$) | C. | [-$\frac{3}{2}$,$\frac{3}{2}$] | D. | [-$\frac{9}{4}$,$\frac{9}{4}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com