Question

5．已知z•$\overline{z}$+（3+$\sqrt{3}$i）z+（3-$\sqrt{3}$i）$\overline{z}$+9=0，求|z-$\sqrt{3}$i|的最大值与最小值．

Answer 1

分析 设z=a+bi（a，b∈R），代入z•$\overline{z}$+（3+$\sqrt{3}$i）z+（3-$\sqrt{3}$i）$\overline{z}$+9=0，得z的轨迹是以（-3，$\sqrt{3}$）为圆心，以$\sqrt{3}$为半径的圆，画出图形，数形结合得答案．

解答 解：设z=a+bi（a，b∈R），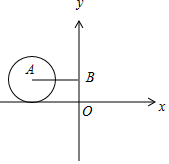
由z•$\overline{z}$+（3+$\sqrt{3}$i）z+（3-$\sqrt{3}$i）$\overline{z}$+9=0，得
a²+b²+（3+$\sqrt{3}$i）（a+bi）+（3-$\sqrt{3}$i）（a-bi）+9=0，
即${a}^{2}+{b}^{2}+6a-2\sqrt{3}b+9=0$，
∴$（a+3）^{2}+（b-\sqrt{3}）^{2}=3$．
则z的轨迹是以（-3，$\sqrt{3}$）为圆心，以$\sqrt{3}$为半径的圆．
如图，
则|z-$\sqrt{3}$i|的最大值为3+$\sqrt{3}$，最小值为3-$\sqrt{3}$．

点评 本题考查复数的代数表示法及其几何意义，考查了数学转化思想方法和数形结合的解题思想方法，是中档题．