Question

9．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的长轴长为4，焦距为2$\sqrt{2}$．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过动点M（0，m）（m＞0）的直线交x轴于点N，交C于点A，P（P在第一象限），且M是线段PN的中点，过点P作x轴的垂线交C于另一点Q，延长QM交C于点B．
（ⅰ）设直线PM，QM的斜率分别为k，k′，证明$\frac{k′}{k}$为定值；
（ⅱ）求直线AB的斜率的最小值．

Answer 1

分析 （Ⅰ）利用已知条件求出椭圆的几何量，即可求解椭圆C的方程；
（Ⅱ）（ⅰ）设出N的坐标，求出PQ坐标，求出直线的斜率，即可推出结果
（ⅱ）求出直线PM，QM的方程，然后求解B，A坐标，利用AB的斜率求解最小值．

解答 解：（Ⅰ）椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的长轴长为4，焦距为2$\sqrt{2}$．可得a=2，c=$\sqrt{2}$，b=$\sqrt{2}$，
可得椭圆C的方程：$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$；
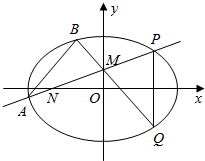
（Ⅱ）过动点M（0，m）（m＞0）的直线交x轴于点N，交C于点A，P（P在第一象限），设N（-t，0）t＞0，M是线段PN的中点，则P（t，2m），过点P作x轴的垂线交C于另一点Q，Q（t，-2m），
（ⅰ）证明：设直线PM，QM的斜率分别为k，k′，
k=$\frac{2m-m}{t-0}$=$\frac{m}{t}$，k′=$\frac{-2m-m}{t-0}$=-$\frac{3m}{t}$，
$\frac{k′}{k}$=$\frac{\frac{-3m}{t}}{\frac{m}{t}}$=-3．为定值；
（ⅱ）由题意可得$\frac{{t}^{2}}{4}+\frac{{m}^{2}}{2}=1$，m²=4-$\frac{1}{2}$t²，QM的方程为：y=-3kx+m，
PN的方程为：y=kx+m，
联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\\{y=kx+m}\end{array}\right.$，可得：x²+2（kx+m）²=4，
即：（1+2k²）x²+4mkx+2m²-4=0
可得x_A=$\frac{2（{m}^{2}-2）}{（2{k}^{2}+1）{x}_{Q}}$，y_A=$\frac{2（{m}^{2}-2）}{（2{k}^{2}+1）{x}_{Q}}$+m，
同理解得x_B=$\frac{2（{m}^{2}-2）}{（18{k}^{2}+1）{x}_{Q}}$，
y_B=$\frac{-6k（{m}^{2}-2）}{（18{k}^{2}+1）{x}_{Q}}+m$，
x_A-x_B=$\frac{2（{m}^{2}-2）}{（2{k}^{2}+1）{x}_{Q}}$k-$\frac{2（{m}^{2}-2）}{（18{k}^{2}+1）{x}_{Q}}$=$\frac{-32{k}^{2}（{m}^{2}-2）}{（18{k}^{2}+1）（2{k}^{2}+1）{x}_{Q}}$，

y_A-y_B=$\frac{2（{m}^{2}-2）}{（2{k}^{2}+1）{x}_{Q}}$k+m-（$\frac{-6k（{m}^{2}-2）}{（18{k}^{2}+1）{x}_{Q}}+m$）=$\frac{-8k（6{k}^{2}+1）（{m}^{2}-2）}{（18{k}^{2}+1）（2{k}^{2}+1）{x}_{Q}}$，
k_AB=$\frac{{y}_{B}-{y}_{A}}{{x}_{B}-{x}_{A}}$=$\frac{6{k}^{2}+1}{4k}$=$\frac{1}{4}（6k+\frac{1}{k}）$，由m＞0，x₀＞0，可知k＞0，
所以6k+$\frac{1}{k}$$≥2\sqrt{6}$，当且仅当k=$\frac{\sqrt{6}}{6}$时取等号．
此时$\frac{m}{\sqrt{4-8{m}^{2}}}=\frac{\sqrt{6}}{6}$，即m=$\frac{\sqrt{14}}{7}$，符合题意．
所以，直线AB的斜率的最小值为：$\frac{\sqrt{6}}{2}$．

点评 本题考查椭圆方程的综合应用，椭圆方程的求法，直线与椭圆的位置关系的应用，考查转化思想以及计算能力．