
分析 对任意n∈N*,Sn∈{2,3},列举出n=1,2,3,4的情况,归纳可得n>4后都为0或1或-1,则k的最大个数为4.
解答 解:对任意n∈N*,Sn∈{2,3},可得
当n=1时,a1=S1=2或3;
若n=2,由S2∈{2,3},可得数列的前两项为2,0;或2,1;或3,0;或3,-1;
若n=3,由S3∈{2,3},可得数列的前三项为2,0,0;或2,0,1;
或2,1,0;或2,1,-1;或3,0,0;或3,0,-1;或3,1,0;或3,1,-1;
若n=4,由S3∈{2,3},可得数列的前四项为2,0,0,0;或2,0,0,1;
或2,0,1,0;或2,0,1,-1;或2,1,0,0;或2,1,0,-1;
或2,1,-1,0;或2,1,-1,1;或3,0,0,0;或3,0,0,-1;
或3,0,-1,0;或3,0,-1,1;或3,-1,0,0;或3,-1,0,1;
或3,-1,1,0;或3,-1,1,-1;
…
即有n>4后一项都为0或1或-1,则k的最大个数为4,
不同的四个数均为2,0,1,-1,或3,0,1,-1.
故答案为:4.
点评 本题考查数列与集合的关系,考查分类讨论思想方法,注意运用归纳思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ①和②均为真命题 | B. | ①和②均为假命题 | ||
| C. | ①为真命题,②为假命题 | D. | ①为假命题,②为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | -$\frac{\sqrt{10}}{10}$ | D. | -$\frac{3\sqrt{10}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
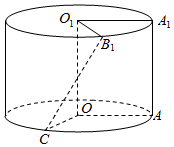 将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图,$\widehat{AC}$长为$\frac{2}{3}$π,$\widehat{A1B1}$长为$\frac{π}{3}$,其中B1与C在平面AA1O1O的同侧.
将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图,$\widehat{AC}$长为$\frac{2}{3}$π,$\widehat{A1B1}$长为$\frac{π}{3}$,其中B1与C在平面AA1O1O的同侧.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
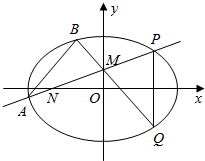 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为4,焦距为2$\sqrt{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为4,焦距为2$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com