
| A. | $\frac{3\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | -$\frac{\sqrt{10}}{10}$ | D. | -$\frac{3\sqrt{10}}{10}$ |
分析 作出图形,令∠DAC=θ,依题意,可求得cosθ=$\frac{AD}{AC}$=$\frac{\frac{a}{3}}{\sqrt{(\frac{1}{3}a)^{2}(\frac{2a}{3})^{2}}}$=$\frac{\sqrt{5}}{5}$,sinθ=$\frac{2\sqrt{5}}{5}$,利用两角和的余弦即可求得答案.
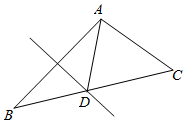
解答 解:设△ABC中角A、B、C、对应的边分别为a、b、c,AD⊥BC于D,令∠DAC=θ,
∵在△ABC中,B=$\frac{π}{4}$,BC边上的高AD=h=$\frac{1}{3}$BC=$\frac{1}{3}$a,
∴BD=AD=$\frac{1}{3}$a,CD=$\frac{2}{3}$a,
在Rt△ADC中,cosθ=$\frac{AD}{AC}$=$\frac{\frac{a}{3}}{\sqrt{(\frac{1}{3}a)^{2}+(\frac{2a}{3})^{2}}}$=$\frac{\sqrt{5}}{5}$,故sinθ=$\frac{2\sqrt{5}}{5}$,
∴cosA=cos($\frac{π}{4}$+θ)=cos$\frac{π}{4}$cosθ-sin$\frac{π}{4}$sinθ=$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{5}}{5}$-$\frac{\sqrt{2}}{2}$×$\frac{2\sqrt{5}}{5}$=-$\frac{\sqrt{10}}{10}$.
故选:C.
点评 本题考查解三角形中,作出图形,令∠DAC=θ,利用两角和的余弦求cosA是关键,也是亮点,属于中档题.


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 △ABC中,角A、B、C所对的边分别为a、b、c,且2acosB=3b-2bcosA.
△ABC中,角A、B、C所对的边分别为a、b、c,且2acosB=3b-2bcosA.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{2}{3}$] | B. | [$\frac{2}{3}$,$\frac{3}{4}$] | C. | [$\frac{1}{3}$,$\frac{2}{3}$]∪{$\frac{3}{4}$} | D. | [$\frac{1}{3}$,$\frac{2}{3}$)∪{$\frac{3}{4}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | N(-1,2,3) | B. | N(1,-2,3) | C. | N(1,2,-3) | D. | N(1,-2,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k<9 | B. | 9<k<16 | C. | 16<k<25 | D. | k>25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com