Question

2．△ABC中，角A、B、C所对的边分别为a、b、c，且2acosB=3b-2bcosA．
（1）求$\frac{b}{c}$的值；
（2）设AB的中垂线交BC于D，若cos∠ADC=$\frac{17}{32}$，b=2，求△ABC的面积．

Answer 1

分析 （1）根据正弦定理、两角和的正弦公式化简已知的式子，再由正弦定理求出$\frac{b}{c}$的值；
（2）根据条件和二倍角的余弦公式求出sinB的值，由平方关系求出cosB的值，由余弦定理求出a，由条件进行取舍，代入三角形的面积公式求出△ABC的面积．

解答 解：（1）∵2acosB=3b-2bcosA，
∴2sinAcosB=3sinB-2sinBcosA
∴2sin（A+B）=3sinB，则2sinC=3sinB，
由正弦定理得，$\frac{b}{c}$=$\frac{sinB}{sinC}$=$\frac{2}{3}$；
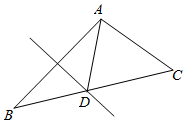
（2）∵AB的中垂线交BC于D，∴DA=DB，则∠B=∠BAD，
∴∠ADC=∠B+∠BAD=2∠B，
∵cos∠ADC=$\frac{17}{32}$，∴cos∠ADC=1-2sin²B=$\frac{17}{32}$，
解得sinB=$\frac{\sqrt{15}}{8}$，
由B是锐角得，cosB=$\sqrt{1-si{n}^{2}B}$=$\frac{7}{8}$，
∵在△ABC中，b=2，且$\frac{b}{c}$=$\frac{2}{3}$，∴c=3，
由余弦定理得，b²=a²+c²-2accosB，
∴$4={a}^{2}+9-2×3×a×\frac{7}{8}$，解得a=4或$\frac{5}{4}$，
∵BD=$\frac{\frac{3}{2}}{cosB}$=$\frac{12}{7}$＞$\frac{5}{4}$，∴a=$\frac{5}{4}$舍去，
∴△ABC的面积S=$\frac{1}{2}acsinB$=$\frac{1}{2}×4×3×\frac{\sqrt{15}}{8}$=$\frac{3\sqrt{15}}{4}$．

点评 本题考查了正弦、余弦定理，两角和的正弦公式，三角形的面积公式的应用，注意结合条件进行取舍以及边角的转化，属于中档题．