
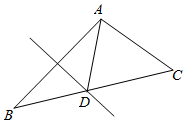
 如图,菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=CF,EF交BD于点H,将△DEF沿EF折到△D′EF的位置.
如图,菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=CF,EF交BD于点H,将△DEF沿EF折到△D′EF的位置.分析 (1)根据直线平行的性质以菱形对角线垂直的性质进行证明即可.
(2)根据条件求出底面五边形的面积,结合平行线段的性质证明OD′是五棱锥D′-ABCFE的高,即可得到结论.
解答 (Ⅰ)证明:∵菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=CF,
∴EF∥AC,且EF⊥BD
将△DEF沿EF折到△D′EF的位置,
则D′H⊥EF,
∵EF∥AC,
∴AC⊥HD′;
(Ⅱ)若AB=5,AC=6,则AO=3,B0=OD=4,
∵AE=$\frac{5}{4}$,AD=AB=5,
∴DE=5-$\frac{5}{4}$=$\frac{15}{4}$,
∵EF∥AC,
∴$\frac{DE}{AD}$=$\frac{EH}{AO}$=$\frac{DH}{OD}$=$\frac{\frac{15}{4}}{5}$=$\frac{3}{4}$,
∴EH=$\frac{9}{4}$,EF=2EH=$\frac{9}{2}$,DH=3,OH=4-3=1,
∵HD′=DH=3,OD′=2$\sqrt{2}$,
∴满足HD′2=OD′2+OH2,
则△OHD′为直角三角形,且OD′⊥OH,
又OD′⊥AC,AC∩OH=O,
即OD′⊥底面ABCD,
即OD′是五棱锥D′-ABCFE的高.
底面五边形的面积S=$\frac{1}{2}×AC•OB$+$\frac{(EF+AC)•OH}{2}$=$\frac{1}{2}×6×4$+$\frac{(\frac{9}{2}+6)×1}{2}$=12+$\frac{21}{4}$=$\frac{69}{4}$,
则五棱锥D′-ABCFE体积V=$\frac{1}{3}$S•OD′=$\frac{1}{3}$×$\frac{69}{4}$×2$\sqrt{2}$=$\frac{23\sqrt{2}}{2}$.
点评 本题主要考查空间直线和平面的位置关系的判断,以及空间几何体的体积,根据线面垂直的判定定理以及五棱锥的体积公式是解决本题的关键.本题的难点在于证明OD′是五棱锥D′-ABCFE的高.考查学生的运算和推理能力.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | {4,8} | B. | {0,2,6} | C. | {0,2,6,10} | D. | {0,2,4,6,8,10} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 △ABC中,角A、B、C所对的边分别为a、b、c,且2acosB=3b-2bcosA.
△ABC中,角A、B、C所对的边分别为a、b、c,且2acosB=3b-2bcosA.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{2}{3}$] | B. | [$\frac{2}{3}$,$\frac{3}{4}$] | C. | [$\frac{1}{3}$,$\frac{2}{3}$]∪{$\frac{3}{4}$} | D. | [$\frac{1}{3}$,$\frac{2}{3}$)∪{$\frac{3}{4}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | N(-1,2,3) | B. | N(1,-2,3) | C. | N(1,2,-3) | D. | N(1,-2,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com