
分析 解法一:对2个条件关系式分别进行和差化积,再相除可得tan$\frac{x+y}{2}$的值,再利用万能公式可得答案;
解法二:由$\left\{\begin{array}{l}{cosx-cosy=\frac{1}{2}}\\{sinx-siny=\frac{1}{3}}\end{array}\right.$得$\left\{\begin{array}{l}{cos[(x+y)-y]-cos[(x+y)-x]=\frac{1}{2}①}\\{sin[(x+y)-y]-sin[(x+y)-x]=\frac{1}{3}②}\end{array}\right.$;
再分别化简①、②,得出关于sin(x+y)与sin(x+y)的二元一次方程组,再求sin(x+y)的值.
解答 解法一:由cosx-cosy=$\frac{1}{2}$,得-2sin$\frac{x+y}{2}$sin$\frac{x-y}{2}$=$\frac{1}{2}$①,
由sinx-siny=$\frac{1}{3}$,得2cos$\frac{x+y}{2}$sin$\frac{x-y}{2}$=$\frac{1}{3}$②;
$\frac{①}{②}$得,-tan$\frac{x+y}{2}$=$\frac{3}{2}$,即tan$\frac{x+y}{2}$=-$\frac{3}{2}$;
∴sin(x+y)=$\frac{2tan\frac{x+y}{2}}{1{+tan}^{2}\frac{x+y}{2}}$=$\frac{2×(-\frac{3}{2})}{1{+(-\frac{3}{2})}^{2}}$=-$\frac{12}{13}$.
解法二:由$\left\{\begin{array}{l}{cosx-cosy=\frac{1}{2}}\\{sinx-siny=\frac{1}{3}}\end{array}\right.$,得$\left\{\begin{array}{l}{cos[(x+y)-y]-cos[(x+y)-x]=\frac{1}{2}①}\\{sin[(x+y)-y]-sin[(x+y)-x]=\frac{1}{3}②}\end{array}\right.$;
由①得,[cos(x+y)]cosy+sin(x+y)siny]-[cos(x+y)cosx+sin(x+y)sinx]=$\frac{1}{2}$,
即cos(x+y)(cosy-cosx)+sin(x+y)(siny-sinx)=$\frac{1}{2}$,
整理得,-$\frac{cos(x+y)}{2}$-$\frac{sin(x+y)}{3}$=$\frac{1}{2}$,
即2sin(x+y)+3cos(x+y)=-3③;
由②得,[sin(x+y)cosy-cos(x+y)siny]-[sin(x+y)cosx-cos(x+y)sinx]=$\frac{1}{3}$,
即sin(x+y)(cosy-cosx)+cos(x+y)(sinx-siny)=$\frac{1}{3}$,
整理得,-$\frac{sin(x+y)}{2}$+$\frac{cos(x+y)}{3}$=$\frac{1}{3}$,
即3sin(x+y)-2cos(x+y)=-2④;
由③④联立,消去cos(x+y),得sin(x+y)=-$\frac{12}{13}$.
点评 本题考查了三角函数的恒等变换与应用问题,也考查了构造法与解方程组的问题,是基础题目.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
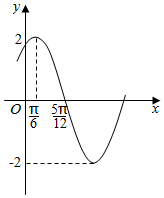 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示:
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=CF,EF交BD于点H,将△DEF沿EF折到△D′EF的位置.
如图,菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=CF,EF交BD于点H,将△DEF沿EF折到△D′EF的位置.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,6} | B. | {3,6} | C. | {1,3,4,5} | D. | {1,2,4,6} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com