
分析 (Ⅰ)求出原函数的导函数,然后对a分类分析导函数的符号,由导函数的符号确定原函数的单调性;
(Ⅱ)构造函数F(x)=f(x)-f′(x),令g(x)=x-lnx,h(x)=$\frac{3}{x}+\frac{1}{{x}^{2}}$$-\frac{2}{{x}^{3}}-1$.则F(x)=f(x)-f′(x)=g(x)+h(x),利用导数分别求g(x)与h(x)的最小值得到F(x)>$\frac{3}{2}$恒成立.由此可得f(x)>f′(x)+$\frac{3}{2}$对于任意的x∈[1,2]成立.
解答 (Ⅰ)解:由f(x)=a(x-lnx)+$\frac{2x-1}{{x}^{2}}$,
得f′(x)=a(1-$\frac{1}{x}$)+$\frac{2{x}^{2}-(2x-1)•2x}{{x}^{4}}$
=$\frac{ax-a}{x}+\frac{2-2x}{{x}^{3}}$=$\frac{a{x}^{3}-a{x}^{2}+2-2x}{{x}^{3}}=\frac{(x-1)(a{x}^{2}-2)}{{x}^{3}}$(x>0).
若a≤0,则ax2-2<0恒成立,
∴当x∈(0,1)时,f′(x)>0,f(x)为增函数,
当x∈(1,+∞)时,f′(x)<0,f(x)为减函数;
当a>0,若0<a<2,当x∈(0,1)和($\frac{\sqrt{2a}}{a}$,+∞)时,f′(x)>0,f(x)为增函数,
当x∈(1,$\frac{\sqrt{2a}}{a}$)时,f′(x)<0,f(x)为减函数;
若a=2,f′(x)≥0恒成立,f(x)在(0,+∞)上为增函数;
若a>2,当x∈(0,$\frac{\sqrt{2a}}{a}$)和(1,+∞)时,f′(x)>0,f(x)为增函数,
当x∈($\frac{\sqrt{2a}}{a}$,1)时,f′(x)<0,f(x)为减函数;
(Ⅱ)解:∵a=1,
令F(x)=f(x)-f′(x)=x-lnx$+\frac{2}{x}$$-\frac{1}{{x}^{2}}$-1$+\frac{2}{{x}^{2}}+\frac{1}{x}-\frac{2}{{x}^{3}}$=x-lnx+$\frac{3}{x}+\frac{1}{{x}^{2}}$$-\frac{2}{{x}^{3}}-1$.
令g(x)=x-lnx,h(x)=$\frac{3}{x}+\frac{1}{{x}^{2}}$$-\frac{2}{{x}^{3}}-1$.
则F(x)=f(x)-f′(x)=g(x)+h(x),
由$g′(x)=\frac{x-1}{x}≥0$,可得g(x)≥g(1)=1,当且仅当x=1时取等号;
又$h′(x)=\frac{-3{x}^{2}-2x+6}{{x}^{4}}$,
设φ(x)=-3x2-2x+6,则φ(x)在[1,2]上单调递减,
且φ(1)=1,φ(2)=-10,
∴在[1,2]上存在x0,使得x∈(1,x0) 时φ(x0)>0,x∈(x0,2)时,φ(x0)<0,
∴函数h(x)在(1,x0)上单调递增;在(x0,2)上单调递减,
由于h(1)=1,h(2)=$\frac{1}{2}$,因此h(x)≥h(2)=$\frac{1}{2}$,当且仅当x=2取等号,
∴f(x)-f′(x)=g(x)+h(x)>g(1)+h(2)=$\frac{3}{2}$,
∴F(x)>$\frac{3}{2}$恒成立.
即f(x)>f′(x)+$\frac{3}{2}$对于任意的x∈[1,2]成立.
点评 本题考查利用导数加以函数的单调性,考查了利用导数求函数的最值,考查了分类讨论的数学思想方法和数学转化思想方法,是压轴题.


科目:高中数学 来源: 题型:选择题
| A. | ①和②均为真命题 | B. | ①和②均为假命题 | ||
| C. | ①为真命题,②为假命题 | D. | ①为假命题,②为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的最小正周期是2π | B. | 函数f(x)在定义域内是奇函数 | ||
| C. | 函数f(x)在区间[0,$\frac{π}{2}$]上是减函数 | D. | 函数f(x)的图象关于直线x=-$\frac{π}{4}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=CF,EF交BD于点H,将△DEF沿EF折到△D′EF的位置.
如图,菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=CF,EF交BD于点H,将△DEF沿EF折到△D′EF的位置.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | -$\frac{\sqrt{10}}{10}$ | D. | -$\frac{3\sqrt{10}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
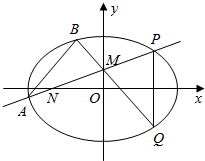 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为4,焦距为2$\sqrt{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为4,焦距为2$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com