
分析 (Ⅰ)根据椭圆的短轴端点C与左右焦点F1、F2构成等腰直角三角形,结合直线l与椭圆E只有一个交点,
利用判别式△=0,即可求出椭圆E的方程和点T的坐标;
(Ⅱ)【解法一】作伸缩变换,令x′=x,y′=$\sqrt{2}$y,把椭圆E变为圆E′,利用圆幂定理求出λ的值,
从而证明命题成立.
【解法二】设出点P的坐标,根据l′∥OT写出l′的参数方程,代入椭圆E的方程中,整理得出方程,
再根据参数的几何意义求出|PT|2、|PA|和|PB|,由|PT|2=λ|PA|•|PB|求出λ的值.
解答 解:(Ⅰ)设短轴一端点为C(0,b),左右焦点分别为F1(-c,0),F2(c,0),其中c>0,
则c2+b2=a2;
由题意,△F1F2C为直角三角形,
∴${{{|F}_{1}F}_{2}|}^{2}$=${{|F}_{1}C|}^{2}$+${{|F}_{2}C|}^{2}$,解得b=c=$\frac{\sqrt{2}}{2}$a,
∴椭圆E的方程为$\frac{{x}^{2}}{{2b}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1;
代入直线l:y=-x+3,可得3x2-12x+18-2b2=0,
又直线l与椭圆E只有一个交点,则△=122-4×3(18-2b2)=0,解得b2=3,
∴椭圆E的方程为$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1;
由b2=3,解得x=2,则y=-x+3=1,所以点T的坐标为(2,1);
(Ⅱ)【解法一】作伸缩变换,令x′=x,y′=$\sqrt{2}$y,
则椭圆E变为圆E′:x′2+y′2=6,
设此时P、A、B、T对应的点分别为P′、A′、B′、T′,
如图所示;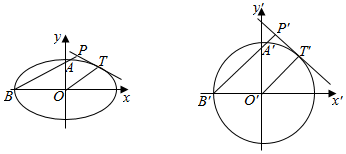
则$\frac{{|P′T′|}^{2}}{{|PT|}^{2}}$=$\frac{1{+2×(-1)}^{2}}{1{+(-1)}^{2}}$=$\frac{3}{2}$,
$\frac{|P′A′|•|P′B′|}{|PA|•|PB|}$=$\frac{1+2{×(\frac{1}{2})}^{2}}{1{+(\frac{1}{2})}^{2}}$=$\frac{6}{5}$,
两式相比,得$\frac{{|P′T′|}^{2}}{{|PT|}^{2}}$:$\frac{|P′A′|•|P′B′|}{|PA|•|PB|}$=$\frac{5}{4}$,
由圆幂定理得,|P′T′|2=|P′A′|•|P′B′|,
所以$\frac{{|PT|}^{2}}{|PA|•|PB|}$=$\frac{4}{5}$,即λ=$\frac{4}{5}$,原命题成立.
【解法二】设P(x0,3-x0)在l上,由kOT=$\frac{1}{2}$,l′平行OT,
得l′的参数方程为$\left\{\begin{array}{l}{x{=x}_{0}+2t}\\{y=3{-x}_{0}+t}\end{array}\right.$,
代入椭圆E中,得${{(x}_{0}+2t)}^{2}$+2${(3{-x}_{0}+t)}^{2}$=6,
整理得2t2+4t+${{x}_{0}}^{2}$-4x0+4=0;
设两根为tA,tB,则有tA•tB=$\frac{{{(x}_{0}-2)}^{2}}{2}$;
而|PT|2=${(\sqrt{{{(x}_{0}-2)}^{2}{+(3{-x}_{0}-1)}^{2}})}^{2}$=2${{(x}_{0}-2)}^{2}$,
|PA|=$\sqrt{{{[(x}_{0}+{2t}_{A}){-x}_{0}]}^{2}{+[(3{-x}_{0}{+t}_{A})-(3{-x}_{0})]}^{2}}$=|$\sqrt{5}$tA|,
|PB|=$\sqrt{{[{(x}_{0}+{2t}_{B}){-x}_{0}]}^{2}{+[(3{-x}_{0}{+t}_{B})-(3{-x}_{0})]}^{2}}$=|$\sqrt{5}$tB|,
且|PT|2=λ|PA|•|PB|,
∴λ=$\frac{{|PT|}^{2}}{|PA|•|PB|}$=$\frac{{2{(x}_{0}-2)}^{2}}{{\frac{5}{2}{(x}_{0}-2)}^{2}}$=$\frac{4}{5}$,
即存在满足题意的λ值.
点评 本题考查了椭圆的几何性质的应用问题,也考查了直线与椭圆方程的综合应用问题,考查了参数方程的应用问题,是难题.


科目:高中数学 来源: 题型:解答题
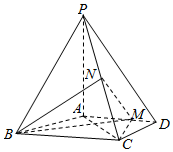 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com