
分析 (1)从-3,-2,-1,0,5,6,7这七个数中任取两数,先求出基本事件总数,再求出积为0,包含的基本事件个数,由此能求出积为0的概率.
(2)求出积为负数,包含的基本事件个数,由此能求出积为负数的概率.
(3)求出积为正数,包含的基本事件个数,由此能求出积为正数的概率.
解答 解:(1)从-3,-2,-1,0,5,6,7这七个数中任取两数,
基本事件总数n=${C}_{7}^{2}$=21,
积为0,包含的基本事件个数m=6,
∴积为0的概率p1=$\frac{6}{21}$=$\frac{2}{7}$.
(2)积为负数,包含的基本事件个数m′=3×3=9,
∴积为负数的概率p2=$\frac{{m}^{'}}{n}$=$\frac{9}{21}$=$\frac{3}{7}$.
(3)积为正数,包含的基本事件个数m''=${C}_{3}^{2}+{C}_{3}^{2}$=6,
∴积为正数的概率p3=$\frac{{m}^{''}}{n}$=$\frac{6}{21}=\frac{2}{7}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
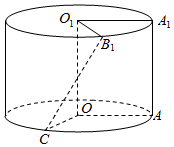 将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图,$\widehat{AC}$长为$\frac{2}{3}$π,$\widehat{A1B1}$长为$\frac{π}{3}$,其中B1与C在平面AA1O1O的同侧.
将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图,$\widehat{AC}$长为$\frac{2}{3}$π,$\widehat{A1B1}$长为$\frac{π}{3}$,其中B1与C在平面AA1O1O的同侧.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 年龄x | 0.3 | 1.2 | 1.7 | 1.9 | 2.2 | 2.6 | 3.1 | 3.2 | 3.8 | 4.0 |
| 身高y | 63 | 71 | 76 | 79 | 83 | 87 | 91 | 93 | 97 | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com