
分析 (Ⅰ)根据复合函数的导数公式进行求解即可求f′(x);
(Ⅱ)讨论a的取值,利用分类讨论的数学,结合换元法,以及一元二次函数的最值的性质进行求解;
(Ⅲ)由(I),结合绝对值不等式的性质即可证明:|f′(x)|≤2A.
解答 (I)解:f′(x)=-2asin2x-(a-1)sinx.
(II)当a≥1时,|f(x)|=|acos2x+(a-1)(cosx+1)|≤a|cos2x|+(a-1)|(cosx+1)|≤a|cos2x|+(a-1)(|cosx|+1)|≤a+2(a-1)=3a-2=f(0),因此A=3a-2.
当0<a<1时,f(x)等价为f(x)=acos2x+(a-1)(cosx+1)=2acos2x+(a-1)cosx-1,
令g(t)=2at2+(a-1)t-1,
则A是|g(t)|在[-1,1]上的最大值,g(-1)=a,g(1)=3a-2,
且当t=$\frac{1-a}{4a}$时,g(t)取得极小值,极小值为g($\frac{1-a}{4a}$)=-$\frac{(a-1)^{2}}{8a}$-1=-$\frac{{a}^{2}+6a+1}{8a}$,(二次函数在对称轴处取得极值)
令-1<$\frac{1-a}{4a}$<1,得a<$-\frac{1}{3}$(舍)或a>$\frac{1}{5}$.因此A=3a-2
①当0<a≤$\frac{1}{5}$时,g(t)在(-1,1)内无极值点,|g(-1)|=a,|g(1)|=2-3a,|g(-1)|<|g(1)|,
∴A=2-3a,
②当$\frac{1}{5}$<a<1时,由g(-1)-g(1)=2(1-a)>0,得g(-1)>g(1)>g($\frac{1-a}{4a}$),
又|g($\frac{1-a}{4a}$)|-|g(-1)|=$\frac{(1-a)(1+7a)}{8a}$>0,
∴A=|g($\frac{1-a}{4a}$)|=$\frac{{a}^{2}+6a+1}{8a}$,
综上,A=$\left\{\begin{array}{l}{2-3a,}&{0<a≤\frac{1}{5}}\\{\frac{{a}^{2}+6a+1}{8a},}&{\frac{1}{5}<a<1}\\{3a-2,}&{a≥1}\end{array}\right.$.
(III)证明:由(I)可得:|f′(x)|=|-2asin2x-(a-1)sinx|≤2a+|a-1|,
当0<a≤$\frac{1}{5}$时,|f′(x)|≤1+a≤2-4a<2(2-3a)=2A,
当$\frac{1}{5}$<a<1时,A=$\frac{{a}^{2}+6a+1}{8a}$=$\frac{a}{8}$+$\frac{1}{8a}$+$\frac{3}{4}$≥1,
∴|f′(x)|≤1+a≤2A,
当a≥1时,|f′(x)|≤3a-1≤6a-4=2A,
综上:|f′(x)|≤2A.
点评 本题主要考查函数的导数以及函数最值的应用,求函数的导数,利用函数单调性和导数的关系,以及换元法,转化法转化法转化为一元二次函数是解决本题的关键.综合性较强,难度较大.


科目:高中数学 来源: 题型:选择题
| A. | [2,3] | B. | (-∞,2]∪[3,+∞) | C. | [3,+∞) | D. | (0,2]∪[3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的最小正周期是2π | B. | 函数f(x)在定义域内是奇函数 | ||
| C. | 函数f(x)在区间[0,$\frac{π}{2}$]上是减函数 | D. | 函数f(x)的图象关于直线x=-$\frac{π}{4}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | -$\frac{\sqrt{10}}{10}$ | D. | -$\frac{3\sqrt{10}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
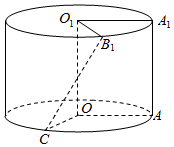 将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图,$\widehat{AC}$长为$\frac{2}{3}$π,$\widehat{A1B1}$长为$\frac{π}{3}$,其中B1与C在平面AA1O1O的同侧.
将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图,$\widehat{AC}$长为$\frac{2}{3}$π,$\widehat{A1B1}$长为$\frac{π}{3}$,其中B1与C在平面AA1O1O的同侧.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com