
【题目】如图,由三棱柱![]() 和四棱锥
和四棱锥![]() 构成的几何体中,
构成的几何体中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() .
.
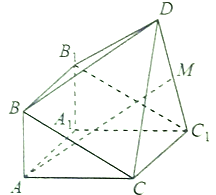
(Ⅰ)求证: ![]() ;
;
(Ⅱ)若![]() 为棱
为棱![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?若存在,求
?若存在,求![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)不存在这样的点.
【解析】试题分析: (Ⅰ)在直三棱柱![]() 中,由
中,由![]() 平面
平面![]() ,推得
,推得![]() ,
,
由平面![]() 平面
平面![]() ,推得
,推得![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,得证.(Ⅱ)如图建立空间直角坐标系
,得证.(Ⅱ)如图建立空间直角坐标系![]() ,写出各点坐标,求出平面
,写出各点坐标,求出平面![]() 的法向量为
的法向量为![]() ,因为
,因为![]() , 所以
, 所以![]() 平面
平面![]() .(Ⅲ)设
.(Ⅲ)设![]() ,
, ![]() ,根据线面角公式列出方程,解得
,根据线面角公式列出方程,解得![]() ,可得结论.
,可得结论.
试题解析:(Ⅰ)证明:在直三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
,
故![]() ,
,
由平面![]() 平面
平面![]() ,且平面
,且平面![]()
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以![]() .
.
(Ⅱ)证明:在直三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
,
所以![]() ,
, ![]() ,
,
又![]() ,
,
所以,如图建立空间直角坐标系![]() ,
,
依据已知条件可得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
由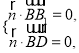 即
即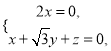
令![]() ,则
,则![]() ,
, ![]() ,于是
,于是![]() ,
,
因为![]() 为
为![]() 中点,所以
中点,所以![]() ,所以
,所以![]() ,
,
由![]() ,可得
,可得![]() ,
,
所以![]() 与平面
与平面![]() 所成角为0,
所成角为0,
即![]() 平面
平面![]() .
.
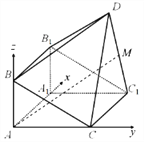
(Ⅲ)解:由(Ⅱ)可知平面![]() 的法向量为
的法向量为![]() .
.
设![]() ,
, ![]() ,
,
则![]() ,
, ![]() .
.
若直线![]() 与平面
与平面![]() 成角为
成角为![]() ,则
,则
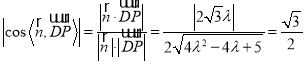 ,
,
解得![]() ,
,
故不存在这样的点.


科目:高中数学 来源: 题型:
【题目】为了促进学生的全面发展,郑州市某中学重视学生社团文化建设,现用分层抽样的方法从“话剧社”,“创客社”、“演讲社”三个金牌社团中抽6人组成社团管理小组,有关数据见下表(单位:人):
社团名称 | 成员人数 | 抽取人数 |
话剧社 | 50 | a |
创客社 | 150 | b |
演讲社 | 100 | c |
(1)求![]() 的值;
的值;
(2)若从“话剧社”,“创客社”,“演讲社”已抽取的6人中任意抽取2人担任管理小组组长,求这2人来自不同社团的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() (
(![]() )与椭圆
)与椭圆![]() :
:![]() 相交所得的弦长为
相交所得的弦长为![]()
(Ⅰ)求抛物线![]() 的标准方程;
的标准方程;
(Ⅱ)设![]() ,
,![]() 是
是![]() 上异于原点
上异于原点![]() 的两个不同点,直线
的两个不同点,直线![]() 和
和![]() 的倾斜角分别为
的倾斜角分别为![]() 和
和![]() ,当
,当![]() ,
,![]() 变化且
变化且![]() 为定值
为定值![]() (
(![]() )时,证明:直线
)时,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲乙两种产品均需用A,B两种原料,已知生产1吨每种产品需原料及每天原料的可用限额如右表所示,如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
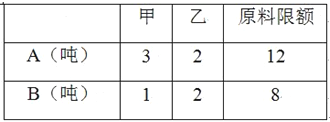
A.18万元 B.17万元 C.16万元 D.12万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(请选做其中一题)
(1)请推导等差数列及等比数列前![]() 项和公式;
项和公式;
(2)如果你在海上航行,请设计一种测量海上两个小岛之间距离的方法并作图说明;
(3)某工厂要建造一个长方形无盖贮水池,其容积为4800立方米,深为3米,如果池底每平米的造价为150元,池壁每平米造价为120元,怎样设计水池能使造价最低?最低总造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过椭圆![]() 上一点
上一点![]() 向
向![]() 轴作垂线,垂足为左焦点
轴作垂线,垂足为左焦点![]() ,
,![]() 分别为
分别为![]() 的右顶点,上顶点,且
的右顶点,上顶点,且![]() ,
,![]() .
.
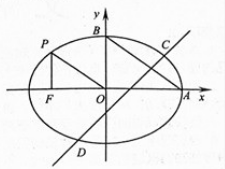
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 为
为![]() 上的两点,若四边形
上的两点,若四边形![]()
![]() 逆时针排列)的对角线
逆时针排列)的对角线![]() 所在直线的斜率为
所在直线的斜率为![]() ,求四边形
,求四边形![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
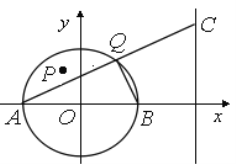
【题目】已知圆![]() ,直线
,直线![]() :x=6,圆
:x=6,圆![]() 与
与![]() 轴相交于点
轴相交于点![]() (如图),点P(-1,2)是圆
(如图),点P(-1,2)是圆![]() 内一点,点
内一点,点![]() 为圆
为圆![]() 上任一点(异于点
上任一点(异于点![]() ),直线
),直线![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)若过点P的直线![]() 与圆
与圆![]() 相交所得弦长等于
相交所得弦长等于![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com