
分析 通过在an2=S2n-1中令n=1、2,计算可知数列的通项an=2n-1,进而问题转化为求f(n)=$\frac{(2n+1)[n+8•(-1)^{n}]}{2n}$的最小值,对n的值分奇数、偶数两种情况讨论即可.
解答 解:∵an2=S2n-1,
∴a12=S1=a1,
又∵an≠0,
∴a1=1,
又∵a22=S3=3a2,
∴a2=3或a2=0(舍),
∴数列{an}的公差d=a2-a1=3-1=2,
∴an=1+2(n-1)=2n-1,
∴不等式$\frac{λ}{{{a_{n+1}}}}$≤$\frac{{n+8•{{(-1)}^n}}}{2n}$对任意的n∈N+恒成立,
即不等式$\frac{λ}{2n+1}$≤$\frac{{n+8•{{(-1)}^n}}}{2n}$对任意的n∈N+恒成立,
∴λ小于等于f(n)=$\frac{(2n+1)[n+8•(-1)^{n}]}{2n}$的最小值,
①当n为奇数时,f(n)=$\frac{(2n+1)(n-8)}{2n}$=n-$\frac{4}{n}$-$\frac{15}{2}$随着n的增大而增大,
∴此时f(n)min=f(1)=1-4-$\frac{15}{2}$=$-\frac{21}{2}$;
②当n为偶数时,f(n)=$\frac{(2n+1)(n+8)}{2n}$=n+$\frac{4}{n}$+$\frac{17}{2}$>$\frac{17}{2}$,
∴此时f(n)min>$\frac{17}{2}$>$-\frac{21}{2}$;
综合①、②可知λ≤$-\frac{21}{2}$,
故答案为:$-\frac{21}{2}$.
点评 本题是一道关于数列与不等式的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
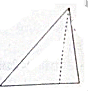 已知一个四棱锥的底面由不等式组$\left\{\begin{array}{l}{x≤0}\\{y≥0}\\{x+y≤2}\\{y-x-4≤0}\end{array}\right.$确定的平面区域构成,其正视图为如图所示的直角三角形(其中虚线长度为$\sqrt{5}$),则此四棱锥的体积是( )
已知一个四棱锥的底面由不等式组$\left\{\begin{array}{l}{x≤0}\\{y≥0}\\{x+y≤2}\\{y-x-4≤0}\end{array}\right.$确定的平面区域构成,其正视图为如图所示的直角三角形(其中虚线长度为$\sqrt{5}$),则此四棱锥的体积是( )| A. | 14 | B. | 7$\sqrt{5}$ | C. | $\frac{14}{3}$ | D. | $\frac{2\sqrt{5}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com