
分析 根据极限的运算性质直接计算即得结论.
解答 解:(1)$\underset{lim}{x→2}$$\frac{{x}^{2}+5}{x-3}$=$\frac{\underset{lim}{x→2}({x}^{2}+5)}{\underset{lim}{x→2}(x-3)}$=$\frac{{2}^{2}+5}{2-3}$=-9;
(2)$\underset{lim}{x→1}$$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$=$\underset{lim}{x→1}$$\frac{(x-1)^{2}}{(x-1)(x+1)}$=$\underset{lim}{x→1}$$\frac{x-1}{x+1}$=$\frac{\underset{lim}{x→1}(x-1)}{\underset{lim}{x→1}(x+1)}$=0;
(3)$\underset{lim}{x→∞}$(1+$\frac{1}{x}$)(2-$\frac{1}{{x}^{2}}$)=$\underset{lim}{x→∞}$(1+$\frac{1}{x}$)•$\underset{lim}{x→∞}$(2-$\frac{1}{{x}^{2}}$)=(1+0)(2-0)=2.
点评 本题考查极限及其运算,注意解题方法的积累,属于基础题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:解答题
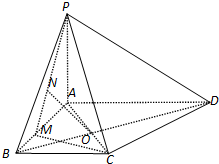 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是梯形,其中AD∥BC,BA⊥AD,AC与BD交于点O,M是AB边上的点,已知PA=AD=4,AB=3,BC=2.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是梯形,其中AD∥BC,BA⊥AD,AC与BD交于点O,M是AB边上的点,已知PA=AD=4,AB=3,BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
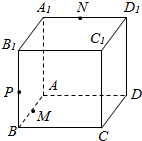 已知M,N,P分别是正方体ABCD-A1B1C1D1的棱,AB,A1D1,BB1上的动点,试过M,N,P三点作正方体ABCD-A1B1C1D1的截面.
已知M,N,P分别是正方体ABCD-A1B1C1D1的棱,AB,A1D1,BB1上的动点,试过M,N,P三点作正方体ABCD-A1B1C1D1的截面.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
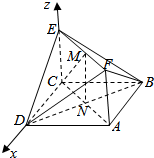 如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=$\sqrt{2}$,AF=1,M是线段EF的中点,N为AC与BD的交点,求点B到平面CMN的距离.
如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=$\sqrt{2}$,AF=1,M是线段EF的中点,N为AC与BD的交点,求点B到平面CMN的距离.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com