练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．已知集合A={x|-1≤x≤2}，B={x|x2-4x≤0}，则A∪B={x|-1≤x≤4}，A∩（∁RB）={x|-1≤x＜0}．

    分析 先求出集合A，B，再求出∁RB，由此能求出A∪B和 A∩（∁RB）．

    解答 解：∵集合A={x|-1≤x≤2}，B={x|x2-4x≤0}={x|0≤x≤4}，
    ∴∁RB={x|x＜0或x＞4}，
    ∴A∪B={x|-1≤x≤4}，A∩（∁RB）={x|-1≤x＜0}．
    故答案为：{x|-1≤x≤4}，{x|-1≤x＜0}．

    点评 本题考查并集、补集、交集的求法，是基础题，解题时要认真审题，注意并集、补集、交集的定义的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    4．设数列{an}的前n项和Sn，数列{Sn}的前n项和为Tn，满足Tn=3Sn-2n，n∈N*．
    （1）求数列{an}的通项公式；
    （2）求证：Sn≥1，n∈N*．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．在平面直角坐标系xOy中，以坐标原点为极轴，x轴正半轴为极轴建立极坐标系，已知曲线C的极坐标方程为：ρ=$\frac{4cosθ}{si{n}^{2}θ}$，直线l的参数方程是$\left\{\begin{array}{l}{x=2+tcosα}\\{y=2+tsinα}\end{array}\right.$（t为参数，0≤α＜π）．
    （1）求曲线C的直角坐标方程；
    （2）设直线l与曲线C交于两点A，B，且线段AB的中点为M（2，2），求α．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知关于x的不等式|x+3|+|x+m|≥2m的解集为R．
    （1）求m的最大值；
    （2）已知a＞0，b＞0，c＞0，且a+b+c=1，求2a2+3b2+4c2的最小值及此时a，b，c的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．设Sn为等差数列{an}的前n项和，若$\frac{{S}_{1}}{{S}_{4}}$=$\frac{1}{10}$，则$\frac{{S}_{3}}{{S}_{5}}$=（　　）
    A．$\frac{2}{5}$B．$\frac{3}{5}$C．$\frac{3}{7}$D．$\frac{4}{7}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

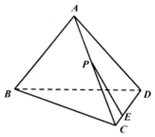    19．如图，已知三棱锥A-BCD的所有棱长均相等，点E满足$\overrightarrow{DE}$=3$\overrightarrow{EC}$，点P在棱AC上运动，设EP与平面BCD所成角为θ，则sinθ的最大值为$\frac{2\sqrt{2}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．函数f（x）=3sin（2x-$\frac{π}{3}$）的图象可以由y=3sin2x的图象（　　）
    A．向右平移$\frac{π}{3}$个单位长度得到B．向左平移$\frac{π}{3}$个单位长度得到
    C．向右平移$\frac{π}{6}$个单位长度得到D．向左平移$\frac{π}{6}$个单位长度得到

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．下面四个命题中的真命题是（　　）
    A．命题“?x≥2，均有x2-3x+2≥0”的否定是：“?x＜2，使得x2-3x+2＜0”
    B．命题“若x2=1，则x=1”的否命题为“若x2=1，则x≠1”
    C．采用系统抽样法从某班按学号抽取5名同学参加活动，学号为5、16、27、38、49的同学均被选出，则该班人数可能为60
    D．在某项测量中，测量结果X服从正态分布N（1，σ2）（σ＞0），若X在（0，1）内取值的概率为0.3，则X在（0，2）内取值的概率为0.6

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知|$\vec a$|=1，|$\vec b$|=$\sqrt{2}$，（$\vec a$-$\vec b$）$⊥\overrightarrow a$，则$\vec a$与$\vec b$的夹角是$\frac{π}{4}$．

    查看答案和解析>>

    同步练习册答案