
分析 利用两个向量的数量积的定义,求得$\vec a$与$\vec b$的夹角的余弦值,可得$\vec a$与$\vec b$的夹角.
解答 解:设$\vec a$与$\vec b$的夹角为θ,θ∈[0,π],则由已知|$\vec a$|=1,|$\vec b$|=$\sqrt{2}$,($\vec a$-$\vec b$)$⊥\overrightarrow a$,
可得($\vec a$-$\vec b$)•$\overrightarrow{a}$=${\overrightarrow{a}}^{2}$-$\overrightarrow{a}•\overrightarrow{b}$=1-1•$\sqrt{2}$•cosθ=0,∴cosθ=$\frac{\sqrt{2}}{2}$,∴θ=$\frac{π}{4}$,
故答案为:$\frac{π}{4}$.
点评 本题主要考查两个向量的数量积的定义,属于基础题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | x0>c | B. | x0>b | C. | x0<c | D. | x0<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{25}$ | B. | -$\frac{24}{25}$ | C. | -$\frac{1}{25}$ | D. | $\frac{1}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
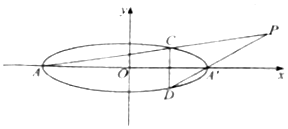 如图所示,椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1的左,右顶点分别为A,A′,线段CD是垂直于椭圆长轴的弦,连接AC,DA′相交于点P,则点P的轨迹方程为$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1.
如图所示,椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1的左,右顶点分别为A,A′,线段CD是垂直于椭圆长轴的弦,连接AC,DA′相交于点P,则点P的轨迹方程为$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com