
 ��ͼ������ABCD�У�AB=2��BC=4���Ծ���ABCD������Ϊԭ�㣬������ABCD������ƽ����BC��ֱ��Ϊx�ᣬ����ֱ������ϵ��
��ͼ������ABCD�У�AB=2��BC=4���Ծ���ABCD������Ϊԭ�㣬������ABCD������ƽ����BC��ֱ��Ϊx�ᣬ����ֱ������ϵ������ ��1����P��x��y������|y-1|•|y+1|=1�����ɵõ����̺켣��
��2����P��x��y����������ɵ�$\sqrt{��x-2��^{2}+{y}^{2}}$=|x+2|+4�������������ɵõ����̺켣��
��3����P��x��y������|y-1|•|y+1|=a|x-2|•|x+2|��������������a���ۣ���a=$\frac{1}{4}$ʱ����a=1ʱ����a$��\frac{1}{4}$��a��1ʱ����������켣���̺켣��
��� 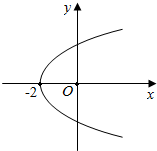 �⣺��1����ͼ����P��x��y������|y-1|•|y+1|=1��
�⣺��1����ͼ����P��x��y������|y-1|•|y+1|=1��
�����y=��$\sqrt{2}$��y=0��
�ʶ���P�Ĺ켣Ϊ����ƽ���ߣ�
��2����P��x��y����������ɵ�$\sqrt{��x-2��^{2}+{y}^{2}}$=|x+2|+4��
��Ϊy2=8��|x+2|+x+2����
����y2=$\left\{\begin{array}{l}{0��x��-2}\\{16��x+2����x��-2}\end{array}\right.$��
��ͼ����ͼ����ʾһ�������ߺ�һ�����ߣ�
��3����P��x��y������|y-1|•|y+1|=a|x-2|•|x+2|��
�����[��y2-1��+a��x2-4��]•[��y2-1��-a��x2-4��]=0��
��ax2-y2=4a-1��ax2+y2=4a+1��a��0����
���е�a=$\frac{1}{4}$ʱ����ʾ�����ֱཻ�ߺ���Բ��
��a=1ʱ����ʾ˫���ߺ�Բ��
��a$��\frac{1}{4}$��a��1ʱ����ʾ˫���ߺ���Բ��
���� ���⿼��켣���̵����Լ����̱�ʾ�Ĺ켣��ͬʱ����ֱ�ߺ�Բ����Բ��˫���ߵķ��̣����÷������۵�˼�뷽���ǽ���Ĺؼ���


 ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ����ϰ�⽭��ϵ�д�
����ϰ�⽭��ϵ�д� ѧ���쳵��������������������ϵ�д�
ѧ���쳵��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{8}{13}$ | B�� | $\frac{4}{3}$ | C�� | $\frac{4}{15}$ | D�� | $\frac{8}{15}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{5}}}{2}$ | B�� | $\frac{{\sqrt{15}}}{3}$ | C�� | $\frac{{\sqrt{10}}}{2}$ | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com