
分析 ①由两角和的正弦函数公式化简解析式可得f(x)=$\sqrt{2}$sin(ωx+$\frac{π}{4}$),结合正弦函数图象解答.
②由两角和的正弦函数公式化简解析式可得f(x)=$\sqrt{2}$sin(ωx+$\frac{π}{4}$),由2kπ-$\frac{π}{2}$≤ωx+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,k∈Z可解得函数f(x)的单调递增区间,结合已知可得:-ω≥$\frac{2kπ-\frac{3π}{4}}{ω}$①,ω≤$\frac{2kπ+\frac{π}{4}}{ω}$②,k∈Z,从而解得k=0,又由ωx+$\frac{π}{4}$=kπ+$\frac{π}{2}$,可解得函数f(x)的对称轴为:x=$\frac{kπ+\frac{π}{4}}{ω}$,k∈Z,结合已知可得:ω2=$\frac{π}{4}$,从而可求ω的值.
解答 解:①若ω=1,f(x)=sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$),
则x+$\frac{π}{4}$=kπ,k∈Z,
故x=kπ-$\frac{π}{4}$(k∈Z),
所以函数f(x)的对称中心是$(kπ-\frac{π}{4},0)(k∈z)$.
故答案是:$(kπ-\frac{π}{4},0)(k∈z)$;
②∵f(x)=sinωx+cosωx=$\sqrt{2}$sin(ωx+$\frac{π}{4}$),
∵函数f(x)在区间(-ω,ω)内单调递增,ω>0
∴2kπ-$\frac{π}{2}$≤ωx+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,k∈Z可解得函数f(x)的单调递增区间为:[$\frac{2kπ-\frac{3π}{4}}{ω}$,$\frac{2kπ+\frac{π}{4}}{ω}$],k∈Z,
∴可得::-ω≥$\frac{2kπ-\frac{3π}{4}}{ω}$①,ω≤$\frac{2kπ+\frac{π}{4}}{ω}$②,k∈Z,
∴解得:0<ω2≤$\frac{3π}{4}$-2kπ且0<ω2≤2kπ+$\frac{π}{4}$,k∈Z,
解得:-$\frac{1}{8}$<k<$\frac{3}{8}$,k∈Z,
∴可解得:k=0,
又∵由ωx+$\frac{π}{4}$=kπ+$\frac{π}{2}$,可解得函数f(x)的对称轴为:x=$\frac{kπ+\frac{π}{4}}{ω}$,k∈Z,
∴由函数y=f(x)的图象关于直线x=ω对称,可得:ω2=$\frac{π}{4}$,可解得:ω=$\frac{\sqrt{π}}{2}$.
故答案为:$\frac{\sqrt{π}}{2}$.
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,考查了正弦函数的图象和性质,正确确定k的值是解题的关键,属于中档题.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | -$\frac{5}{13}$ | D. | $\frac{5}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
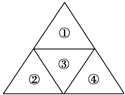 如图,要给①,②,③,④四块区域分别涂上五种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同颜色,则不同的涂色方法种数为( )
如图,要给①,②,③,④四块区域分别涂上五种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同颜色,则不同的涂色方法种数为( )| A. | 320 | B. | 160 | C. | 96 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
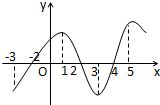
| A. | 在区间(-3,1)内y=f(x)是增函数 | B. | 在区间(1,3)内y=f(x)是减函数 | ||
| C. | 在区间(4,5)内y=f(x)是增函数 | D. | 在x=2时,y=f(x)取得极小值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com