已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$..F为其左焦点.A1.A2分别为其长轴的左右端点.B1为其短轴的一个端点.若原点O到直线FB1的距离$d=\frac{{\sqrt{6}}}{3}$.且椭圆的离心率$e=\frac{{\sqrt{6}}}{3}$,(1)求椭圆的方程,(2)过A1斜率为k的直线l与椭圆交于异于点A1的点C.又过A2作A2D⊥l于D点,ⅰ� 题目和参考答案——青夏教育精英家教网—

17．

已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$，（a＞b＞0），F为其左焦点，A₁，A₂分别为其长轴的左右端点，B₁为其短轴的一个端点，若原点O到直线FB₁的距离$d=\frac{{\sqrt{6}}}{3}$，且椭圆的离心率$e=\frac{{\sqrt{6}}}{3}$；
（1）求椭圆的方程；
（2）过A₁斜率为k（k≠0）的直线l与椭圆交于异于点A₁的点C，又过A₂作A₂D⊥l于D点；
ⅰ．若$\overrightarrow{{A_1}D}=2\overrightarrow{{A_1}C}$，求直线l的方程；
ⅱ．是否存在实数λ，使${|{{A_1}D}|^2}+λ\frac{{{S_{△{A_1}OD}}}}{{{S_{△{A_1}OC}}}}$为常数？如存在，求出λ的值；如不存在，说明理由．

分析（1）由已知可得$\left\{\begin{array}{l}{{c}^{2}={a}^{2}-{b}^{2}}\\{\frac{c}{a}=\frac{\sqrt{6}}{3}}\end{array}\right.$，得导$a=\frac{\sqrt{6}}{2}c，b=\frac{\sqrt{2}}{2}c$，在△FOB₁ 中，由等积法得$\frac{1}{2}bc=\frac{1}{2}a×\frac{\sqrt{6}}{3}$，联立求得a，b的最值，则椭圆方程可求；
（2）ⅰ．设直线l的方程为：y=k（x+$\sqrt{3}$），C（x_C，y_C），D（x_D，y_D），由已知有A₁（$-\sqrt{3}$，0），联立直线方程与椭圆方程，化为关于x的一元二次方程，利用根与系数的关系求得C的横坐标，再求出D点的轨迹方程，联立直线方程与D的轨迹方程，结合向量等式求出C的横坐标，由C得横坐标相等可得k=±1．故直线l的方程可求；
ⅱ．由D点的轨迹方程为：x²+y²=3求得：$|{A}_{1}D{|}^{2}=4（3-\frac{3{k}^{2}}{1+{k}^{2}}）=\frac{12}{1+{k}^{2}}$．再由面积比可得${|{{A_1}D}|^2}+λ\frac{{{S_{△{A_1}OD}}}}{{{S_{△{A_1}OC}}}}$=$\frac{12}{1+{k}^{2}}+λ\frac{|{y}_{D}|}{|{y}_{C}|}=\frac{12}{1+{k}^{2}}+λ\frac{1+3{k}^{2}}{1+{k}^{2}}$=$\frac{12+λ+3λ{k}^{2}}{1+{k}^{2}}$．由${|{{A_1}D}|^2}+λ\frac{{{S_{△{A_1}OD}}}}{{{S_{△{A_1}OC}}}}$为常数，则12+λ=3λ，解得λ=6．

解答解：（1）由$\left\{\begin{array}{l}{{c}^{2}={a}^{2}-{b}^{2}}\\{\frac{c}{a}=\frac{\sqrt{6}}{3}}\end{array}\right.$，得：$a=\frac{\sqrt{6}}{2}c，b=\frac{\sqrt{2}}{2}c$，①
在△FOB₁ 中，由等积法得：$\frac{1}{2}bc=\frac{1}{2}a×\frac{\sqrt{6}}{3}$，②
联立①，②解得$a=\sqrt{3}，b=1，c=\sqrt{2}$．
∴椭圆的方程为：$\frac{{x}^{2}}{3}+{y}^{2}=1$；
（2）ⅰ．设直线l的方程为：y=k（x+$\sqrt{3}$），C（x_C，y_C），D（x_D，y_D），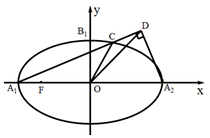
由已知有A₁（$-\sqrt{3}$，0）．
联立$\left\{\begin{array}{l}{y=k（x+\sqrt{3}）}\\{\frac{{x}^{2}}{3}+{y}^{2}=1}\end{array}\right.$，得：$（1+3{k}^{2}）{x}^{2}+6\sqrt{3}{k}^{2}x+9{k}^{2}-3=0$．
∴${x}_{C}=\frac{-6\sqrt{3}{k}^{2}}{1+3{k}^{2}}+\sqrt{3}=\frac{\sqrt{3}-3\sqrt{3}{k}^{2}}{1+3{k}^{2}}$．
由已知：D点的轨迹方程为：x²+y²=3，
联立$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=3}\\{y=k（x+\sqrt{3}）}\end{array}\right.$，得：$（1+{k}^{2}）{x}^{2}+2\sqrt{3}{k}^{2}x+3{k}^{2}-3=0$．
∴${x}_{{A}_{1}}+{x}_{D}=\frac{-2\sqrt{3}{k}^{2}}{1+{k}^{2}}$．
由$\overrightarrow{{A_1}D}=2\overrightarrow{{A_1}C}$，有C为A₁D的中点，
∴$2{x}_{C}={x}_{{A}_{1}}+{x}_{D}$，故$\frac{2\sqrt{3}-6\sqrt{3}{k}^{2}}{1+3{k}^{2}}=\frac{-2\sqrt{3}{k}^{2}}{1+{k}^{2}}$，
∴$\frac{3{k}^{2}-1}{1+3{k}^{2}}=\frac{{k}^{2}}{1+{k}^{2}}$，解得：k=±1．
故直线l的方程为x-y+$\sqrt{3}$=0或x+y+$\sqrt{3}=0$；
ⅱ．由D点的轨迹方程为：x²+y²=3，得：$|{A}_{1}D{|}^{2}=4（3-\frac{3{k}^{2}}{1+{k}^{2}}）=\frac{12}{1+{k}^{2}}$．
又${S}_{△{A}_{1}OD}=\frac{1}{2}{A}_{1}O•|{y}_{D}|$，${S}_{△{A}_{1}OC}=\frac{1}{2}{A}_{1}O•|{y}_{C}|$，
故$\frac{{S}_{△{A}_{1}OD}}{{S}_{△{A}_{1}OC}}=\frac{{y}_{D}}{{y}_{C}}$，由ⅰ可解得：$|{y}_{D}|=\frac{|2\sqrt{3}k|}{1+{k}^{2}}$，$|{y}_{C}|=\frac{|2\sqrt{3}k|}{1+3{k}^{2}}$，
${|{{A_1}D}|^2}+λ\frac{{{S_{△{A_1}OD}}}}{{{S_{△{A_1}OC}}}}$=$\frac{12}{1+{k}^{2}}+λ\frac{|{y}_{D}|}{|{y}_{C}|}=\frac{12}{1+{k}^{2}}+λ\frac{1+3{k}^{2}}{1+{k}^{2}}$=$\frac{12+λ+3λ{k}^{2}}{1+{k}^{2}}$．
要使${|{{A_1}D}|^2}+λ\frac{{{S_{△{A_1}OD}}}}{{{S_{△{A_1}OC}}}}$为常数，则12+λ=3λ，解得λ=6．
故存在实数λ=6，使${|{{A_1}D}|^2}+λ\frac{{{S_{△{A_1}OD}}}}{{{S_{△{A_1}OC}}}}$为常数．

点评本题考查椭圆的简单性质，考查直线与圆、椭圆位置关系的应用，考查逻辑思维能力与推理运算能力，难度较大．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

7．已知抛物线C：y²=8x的焦点为F，准线为1，Q是直线l上的一点，P是直线QF与C的一个交点，若$\overrightarrow{QF}$=4$\overrightarrow{PF}$，则△POF（O为坐标原点）的面积为（　　）

A．

B．

2$\sqrt{3}$

C．

$\sqrt{2}$

D．

2$\sqrt{2}$

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

8．已知实数x，y满足$\left\{\begin{array}{l}{2x+y≤2}\\{x≥0}\\{x+y≥0}\end{array}\right.$，z=（x+1）²+（y+2）²，则z的最小值为（　　）

A．

$\frac{3\sqrt{2}}{2}$

B．

$\frac{9}{2}$

C．

$\sqrt{5}$

D．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

5．设非空集合S={x|m≤x≤l}满足：当x∈S时，有x²∈S．给出以下三个命题：①若m=1，则S={1}；②若$m=-\frac{1}{2}$，则$\frac{1}{4}≤l≤1$；③若$l=\frac{1}{2}$，则$-\frac{{\sqrt{2}}}{2}≤m≤0$．其中正确的命题个数是（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

12．y=cos²x-1，则f（x）是（　　）