
【题目】如图,椭圆![]()
![]() (
(![]() )的离心率是
)的离心率是![]() ,过点
,过点![]() (
(![]() ,
,![]() )的动直线
)的动直线![]() 与椭圆相交于
与椭圆相交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 平行于
平行于![]() 轴时,直线
轴时,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
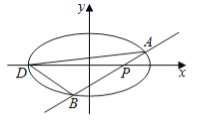
⑴求椭圆![]() 的方程:
的方程:
⑵已知![]() 为椭圆的左端点,问: 是否存在直线
为椭圆的左端点,问: 是否存在直线![]() 使得
使得![]() 的面积为
的面积为![]() ?若不存在,说明理由,若存在,求出直线
?若不存在,说明理由,若存在,求出直线![]() 的方程.
的方程.
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】一盒中放有的黑球和白球,其中黑球4个,白球5个.
(1)从盒中同时摸出两个球,求两球颜色恰好相同的概率.
(2)从盒中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
(3)从盒中不放回的每次摸一球,若取到白球则停止摸球,求取到第三次时停止摸球的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)是奇函数,且满足f(x)=f(x+3),f(-2)=-3.若数列{an}中,a1=-1,且前n项和Sn满足![]() =2×
=2×![]() +1,则f(a5)+f(a6)=________.
+1,则f(a5)+f(a6)=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
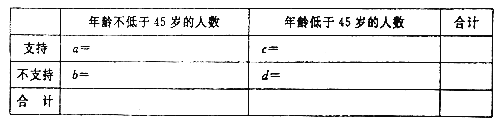
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机抽调了50人,他们年龄的频数分布及支持“生育二胎”人数如下表:

(1)由以上统计数据填下面![]() 列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异;
列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异;
(2)若对年龄在![]() 的被调查人中各随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
的被调查人中各随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?

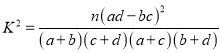
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,六面体ABCDHEFG中,四边形ABCD为菱形,AE,BF,CG,DH都垂直于平面ABCD.若DA=DH=DB=4,AE=CG=3。
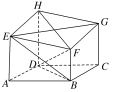
(1)求证:EG⊥DF;
(2)求BE与平面EFGH所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列结论:
,给出下列结论:
(1)若对任意![]() ,且
,且![]() ,都有
,都有![]() ,则
,则![]() 为R上的减函数;
为R上的减函数;
(2)若![]() 为R上的偶函数,且在
为R上的偶函数,且在![]() 内是减函数,
内是减函数, ![]() (-2)=0,则
(-2)=0,则![]() >0解集为(-2,2);
>0解集为(-2,2);
(3)若![]() 为R上的奇函数,则
为R上的奇函数,则![]() 也是R上的奇函数;
也是R上的奇函数;
(4)t为常数,若对任意的![]() ,都有
,都有![]() 则
则![]() 关于
关于![]() 对称。
对称。
其中所有正确的结论序号为_________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为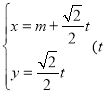 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .且曲线
.且曲线![]() 的左焦点
的左焦点![]() 在直线
在直线![]() 上.
上.
(1)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】化为推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
女性用户:
分值区间 |
|
|
|
|
|
频数 | 20 | 40 | 80 | 50 | 10 |
分值区间 |
|
|
|
|
|
频数 | 45 | 75 | 90 | 60 | 30 |
男性用户:
(1)如果评分不低于70分,就表示该用户对手机“认可”,否则就表示“不认可”,完成下列![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为性别对手机的“认可”有关:
的把握认为性别对手机的“认可”有关:
女性用户 | 男性用户 | 合计 | |
“认可”手机 | |||
“不认可”手机 | |||
合计 |
附:
| 0.05 | 0.01 |
| 3.841 | 6635 |
![]()
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com