
分析 (Ⅰ)求出函数的导数,通过讨论a的范围,解关于导函数的不等式,求出函数的单调区间即可;
(Ⅱ)由h(x)=lnx的图象与直线y=ax有两交点可知;a>0,再根据导数求出切线的斜率,即可求出有2个交点时a的范围.
解答 解:(Ⅰ)f(x)=-$\frac{a}{2}$x2+(a-1)x+lnx,(x>0),
f′(x)=-ax+(a-1)+$\frac{1}{x}$=$\frac{(-ax-1)(x-1)}{x}$,
0<-a<1即-1<a<0时,-$\frac{1}{a}$>1,
令f′(x)>0,解得:x>-$\frac{1}{a}$或0<x<1,
令f′(x)<0,解得:1<x<-$\frac{1}{a}$,
∴f(x)在(0,1)递增,在(1,-$\frac{1}{a}$)递减,在(-$\frac{1}{a}$,+∞)递增,
-a≤0即a≥0时,-ax-1<0,
令f′(x)>0,解得:0<x<1,令f′(x)<0,解得:x>1,
∴f(x)在(0,1)递增,在(1,+∞)递减;
(Ⅱ)若g(x)=$\frac{a}{2}$x2+(1-2a)x+f(x)有且只有两个零点,
即lnx=ax有且只有两个零点,
即h(x)=lnx,y=ax有且只有2个交点,
由h(x)=lnx的图象与直线y=ax有两交点
可知;a>0,
当直线与h(x)=lnx相切时,设切点(x0,lnx0)
∵h′(x)=$\frac{1}{x}$,
∴根据切线的斜率与导数值的关系可知:$\frac{1}{{x}_{0}}$=a,即x0=$\frac{1}{a}$,
代入直线方程可得;ln$\frac{1}{a}$=1,解得:a=$\frac{1}{e}$,
所以函数h(x)=lnx的图象与直线y=ax有两交点,
则0<a<$\frac{1}{e}$.
点评 本题考查函数的单调性问题,考查对数函数的性质,导数的应用,解决交点问题.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 等级 | 优秀 | 合格 | 不合格 |
| 男生(人) | 30 | x | 8 |
| 女生(人) | 30 | 6 | y |
| 男生 | 女生 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,0)∪(2,+∞) | B. | (-2,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-2,0)∪(0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-5,3) | B. | [-5,-4) | C. | [-5,4) | D. | (-4,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
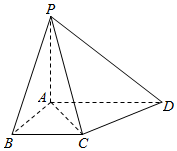 如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,AD∥BC,AD⊥AB,PA=AD=2BC=2AB=2.
如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,AD∥BC,AD⊥AB,PA=AD=2BC=2AB=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com