
分析 由已知得$\frac{1}{{m}^{2}}$-4m2≤-$\frac{3}{{x}^{2}}$-$\frac{2}{x}$+1在x∈[$\frac{3}{2}$,+∞)上恒成立,上由此能求出实数m的取值范围.
解答 解:依据题意得$\frac{{x}^{2}}{{m}^{2}}$-1-4m2(x2-1)≤(x-1)2-1+4(m2-1)在x∈[$\frac{3}{2}$,+∞)上恒定成立,
即$\frac{1}{{m}^{2}}$-4m2≤-$\frac{3}{{x}^{2}}$-$\frac{2}{x}$+1在x∈[$\frac{3}{2}$,+∞)上恒成立.
当x=$\frac{3}{2}$时,函数y=-$\frac{3}{{x}^{2}}$-$\frac{2}{x}$+1取得最小值-$\frac{5}{3}$,
∴$\frac{1}{{m}^{2}}$-4m2≤-$\frac{5}{3}$,即(3m2+1)(4m2-3)≥0,
解得m≤-$\frac{\sqrt{3}}{2}$或m≥$\frac{\sqrt{3}}{2}$,
故答案为:$(-∞,-\frac{{\sqrt{3}}}{2}]∪[\frac{{\sqrt{3}}}{2},+∞)$.
点评 本题考查实数的取值范围的求法,是中档题,解题时要注意函数性质和等价转化思想的合理运用.


科目:高中数学 来源: 题型:选择题

| A. | y=ax和y=loga(-x) | B. | y=ax和$y={log_a}{x^{-1}}$ | ||
| C. | y=a-x和$y={log_a}{x^{-1}}$ | D. | y=a-x和y=loga(-x) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
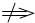 ”.填空:
”.填空: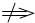 |a|>|b|.
|a|>|b|.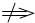 a<-b且a>b.
a<-b且a>b.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{12}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com