
分析 (Ⅰ)利用f(0)=1+a+1=0,求出a,再验证,即可得出不论a为何值时,f(x)不是奇函数;
(Ⅱ)若对任意x∈[0,1],不等式f(x)≤2016恒成立,则a≤2015•2x-$\frac{1}{{2}^{x}}$,求最大值,即可求a的取值范围;
(Ⅲ)令t=$\frac{1}{{2}^{x}}$,利用f(x)有两个不同的零点,可定h(t)=t2+at+1有两个不同的正的零点,即可求a的取值范围.
解答 解:(Ⅰ)假设f(x)是奇函数,则f(0)=1+a+1=0,
∴a=-2,
∵f(1)=$\frac{1}{4}$,f(-1)=1,
∴f(-1)≠f(1)
∴不论a为何值时,f(x)不是奇函数;
(Ⅱ)若对任意x∈[0,1],不等式f(x)≤2016恒成立,则a≤2015•2x-$\frac{1}{{2}^{x}}$.
设g(x)=2015•2x-$\frac{1}{{2}^{x}}$,x∈[0,1],则函数是增函数,
∴a≤g(0)=2014;
(Ⅲ)令t=$\frac{1}{{2}^{x}}$,
∵f(x)有两个不同的零点,
∴h(t)=t2+at+1有两个不同的正的零点,
∴$\left\{\begin{array}{l}{h(0)=1>0}\\{-\frac{a}{2}>0}\\{{a}^{2}-4>0}\end{array}\right.$,
∴a<-2.
点评 本题考查函数的奇偶性,考查恒成立问题,考查函数的零点,正确转化是关键.


科目:高中数学 来源: 题型:选择题
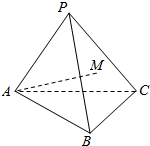 如图,在三棱锥P-ABC中,AB=AC=PB=PC=10,PA=8,BC=12,点M在平面PBC内,且AM=7,设异面直线AM与BC所成角为α,则cosα的最大值为( )
如图,在三棱锥P-ABC中,AB=AC=PB=PC=10,PA=8,BC=12,点M在平面PBC内,且AM=7,设异面直线AM与BC所成角为α,则cosα的最大值为( )| A. | $\frac{1}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{6}{7}$ | D. | $\frac{4\sqrt{3}}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 1 | C. | -1 | D. | 1或-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
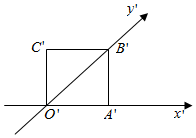 如图,正方形O′A′C′B′的边长为1cm,它是水平放置的一个平面图形的直观图,则它的原图形面积和直观图面积之比是( )
如图,正方形O′A′C′B′的边长为1cm,它是水平放置的一个平面图形的直观图,则它的原图形面积和直观图面积之比是( )| A. | 2$\sqrt{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | 2(1+$\sqrt{3}$) | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com