Question

15．如图，正方体ABC-A₁B₁C₁D₁中，M是棱BB₁的中点．
（1）求直线A₁M与平面AMC₁所成角的正弦值；
（2）求二面角A-MC₁-A₁的余弦值．

Answer 1

分析 （1）首先分别以直线DA，DC，DD₁为x，y，z轴，建立空间直角坐标系，可求出一些点的坐标，设平面AMC₁的法向量为$\overrightarrow{{n}_{1}}=（{x}_{1}，{y}_{1}，{z}_{1}）$，根据$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{AM}=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{A{C}_{1}}=0}\end{array}\right.$，即可求出法向量$\overrightarrow{{n}_{1}}$，设直线A₁M和平面AMC₁所成角为θ，则根据$sinθ=|cos＜\overrightarrow{{n}_{1}}，\overrightarrow{{A}_{1}M}＞|$即可求得直线A₁M与平面AMC₁所成角的正弦值；
（2）设平面A₁MC₁的法向量为$\overrightarrow{{n}_{2}}$=（x₂，y₂，z₂），和求$\overrightarrow{{n}_{1}}$的方法一样可以求出$\overrightarrow{{n}_{2}}$，而法向量$\overrightarrow{{n}_{1}}$，$\overrightarrow{{n}_{2}}$的夹角等于二面角A-MC₁-A₁的大小，从而根据$cos＜\overrightarrow{{n}_{1}}，\overrightarrow{{n}_{2}}＞=\frac{\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}||\overrightarrow{{n}_{2}}|}$即可求得答案．

解答 解：（1）以边DA，DC，DD₁所在直线分别为x，y，z轴，建立如图所示空间直角坐标系，设正方体的边长为2，则：
A（2，0，0），B（2，2，0），B₁（2，2，2），M（2，2，1），C₁（0，2，2），A₁（2，0，2）；
设平面AMC₁的法向量为$\overrightarrow{{n}_{1}}=（{x}_{1}，{y}_{1}，{z}_{1}）$，则$\overrightarrow{{n}_{1}}⊥\overrightarrow{AM}，\overrightarrow{{n}_{1}}⊥\overrightarrow{A{C}_{1}}$；
∴$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{AM}=2{y}_{1}+{z}_{1}=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{A{C}_{1}}=-2{x}_{1}+2{y}_{1}+2{z}_{1}=0}\end{array}\right.$；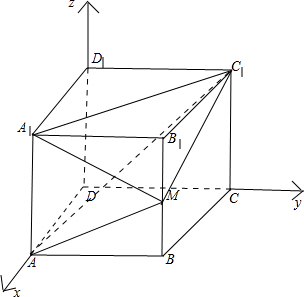
∴$\left\{\begin{array}{l}{{y}_{1}=-{x}_{1}}\\{{z}_{1}=2{x}_{1}}\end{array}\right.$，取x₁=1，则$\overrightarrow{{n}_{1}}=（1，-1，2）$；
设A₁M和平面AMC₁所成角为θ，则：
sinθ=$|cos＜\overrightarrow{{n}_{1}}，\overrightarrow{{A}_{1}M}＞|=\frac{|\overrightarrow{{n}_{1}}•\overrightarrow{{A}_{1}M}|}{|\overrightarrow{{n}_{1}}||\overrightarrow{{A}_{1}M}|}=\frac{4}{\sqrt{6}•\sqrt{5}}=\frac{2\sqrt{30}}{15}$；
（2）设平面A₁MC₁的法向量为$\overrightarrow{{n}_{2}}=（{x}_{2}，{y}_{2}，{z}_{2}）$，则：
$\left\{\begin{array}{l}{\overrightarrow{{n}_{2}}•\overrightarrow{{A}_{1}M}=2{y}_{2}-{z}_{2}=0}\\{\overrightarrow{{n}_{2}}•\overrightarrow{{A}_{1}{C}_{1}}=-2{x}_{2}+2{y}_{2}=0}\end{array}\right.$；
∴$\left\{\begin{array}{l}{{x}_{2}={y}_{2}}\\{{z}_{2}=2{y}_{2}}\end{array}\right.$，取y₂=1，∴$\overrightarrow{{n}_{2}}=（1，1，2）$；
设二面角A-MC₁-A₁的平面角的大小为φ，则：
cosφ=cos＜$\overrightarrow{{n}_{1}}，\overrightarrow{{n}_{2}}$＞=$\frac{\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}||\overrightarrow{{n}_{2}}|}$=$\frac{4}{\sqrt{6}•\sqrt{6}}=\frac{2}{3}$；
∴二面角A-MC₁-A₁的余弦值为$\frac{2}{3}$．

点评 考查建立空间直角坐标系，利用空间向量解决线面角，二面角的问题的方法，平面法向量的概念及求法，线面垂直的判定定理，非零向量垂直的充要条件，要弄清直线方向向量和平面法向量所成角与直线和平面所成角的关系，两平面法向量的夹角和二面角大小的关系，以及向量夹角余弦的坐标公式．