
已知各项均不为零的数列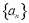 的前
的前 项和为
项和为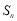 ,且
,且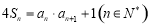 ,其中
,其中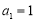 .
.
(1)求证: 成等差数列;
成等差数列;
(2)求证:数列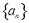 是等差数列;
是等差数列;
(3)设数列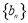 满足
满足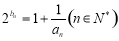 ,且
,且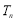 为其前
为其前 项和,求证:对任意正整数
项和,求证:对任意正整数 ,不等式
,不等式 恒成立.
恒成立.
(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
试题分析:(1)利用 进行证明;(2)由
进行证明;(2)由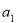 与递推公式求出
与递推公式求出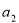 ,结合(1)即可证明数列
,结合(1)即可证明数列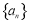 是等差数列;(3)根据题意求出
是等差数列;(3)根据题意求出 ,利用对数的运算选择与累乘法求出
,利用对数的运算选择与累乘法求出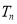 ,再利用数学归纳法证明不等式.
,再利用数学归纳法证明不等式.
试题解析:(1)【解析】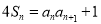 ①;
①;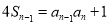 ②;①-②得
②;①-②得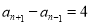 ,得证;
,得证;
(2)【解析】
由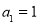 ,得
,得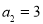 ,结合第(1)问结论,即可得
,结合第(1)问结论,即可得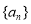 是等差数列;
是等差数列;
(3)【解析】
根据题意,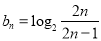 ,
,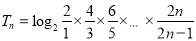 ;
;
要证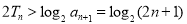 ,即证
,即证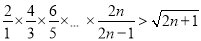 ;
;
当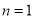 时,
时, 成立;
成立;
假设当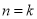 时,
时,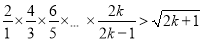 成立;
成立;
当 时,
时,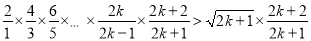
 ;
;
要证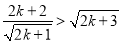 ,即证
,即证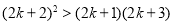 ,展开后显然成立,
,展开后显然成立,
所以对任意正整数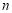 ,不等式
,不等式 恒成立.
恒成立.
考点:1.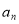 与
与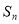 的关系;2.等差数列;3.对数的运算选择;4.数学归纳法.
的关系;2.等差数列;3.对数的运算选择;4.数学归纳法.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源:2014-2015学年广东省广州市毕业班综合测试一理科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知函数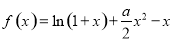
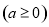 .
.
(1)若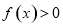 对
对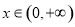 都成立,求
都成立,求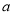 的取值范围;
的取值范围;
(2)已知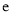 为自然对数的底数,证明:
为自然对数的底数,证明: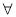
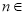 N
N ,
,
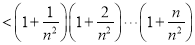
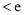 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年云南省弥勒市高三年级模拟测试一文科数学试卷(解析版) 题型:选择题
已知双曲线的一个焦点与抛物线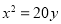 的焦点重合,且其渐近线的方程为
的焦点重合,且其渐近线的方程为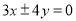 ,则该双曲线的标准方程为( )
,则该双曲线的标准方程为( )
A.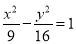 B.
B.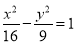 C.
C. D.
D.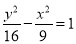
查看答案和解析>>
科目:高中数学 来源:2014-2015学年云南省弥勒市高三年级模拟测试一理科数学试卷(解析版) 题型:选择题
三棱锥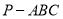 中,
中,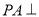 平面
平面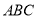 ,
,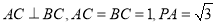 ,则该三棱锥外接球的表面积为( )
,则该三棱锥外接球的表面积为( )
A.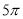 B.
B.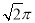 C.
C.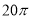 D.
D.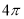
查看答案和解析>>
科目:高中数学 来源:2014-2015学年云南省弥勒市高三年级模拟测试一理科数学试卷(解析版) 题型:选择题
已知双曲线的一个焦点与抛物线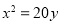 的焦点重合,且其渐近线的方程为
的焦点重合,且其渐近线的方程为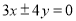 ,则该双曲线的标准方程为( )
,则该双曲线的标准方程为( )
A.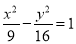 B.
B.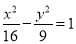 C.
C.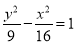 D.
D.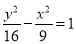
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市虹口区高三上学期期终教学质量监测数学试卷(解析版) 题型:选择题
关于曲线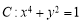 ,给出下列四个命题:
,给出下列四个命题:
①曲线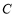 关于原点对称;
关于原点对称;
②曲线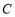 关于直线
关于直线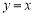 对称
对称
③曲线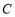 围成的面积大于
围成的面积大于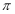
④曲线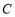 围成的面积小于
围成的面积小于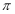
上述命题中,真命题的序号为( )
A.①②③ B.①②④ C.①④ D.①③
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市虹口区高三上学期期终教学质量监测数学试卷(解析版) 题型:填空题
已知 是分别经过
是分别经过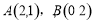 两点的两条平行直线,当
两点的两条平行直线,当 之间的距离最大时,直线
之间的距离最大时,直线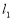 的方程是 .
的方程是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市奉贤区高三上学期期末调研测试数学试卷(解析版) 题型:选择题
定义两个实数间的一种新运算“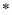 ”:
”: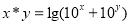 ,
,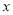 、
、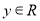 。对于任意实数
。对于任意实数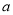 、
、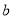 、
、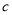 ,给出如下结论:①
,给出如下结论:①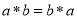 ;②
;②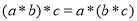 ;③
;③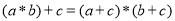 .其中正确结论的个数是 ( )
.其中正确结论的个数是 ( )
A.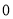 个 B.
个 B.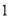 个 C.
个 C.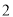 个 D.
个 D.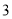 个
个
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省德州市高三上学期2月期末统考理科数学试卷(解析版) 题型:填空题
已知定义在R上的函数f(x)的图象连续不断,若存在常数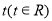 ,
,
使得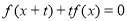 对任意的实数x成立,则称f(x)是回旋函数.
对任意的实数x成立,则称f(x)是回旋函数.
给出下列四个命题:
①常值函数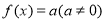 为回旋函数的充要条
为回旋函数的充要条 件是t= -1;
件是t= -1;
②若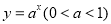 为回旋函数,则t>l;
为回旋函数,则t>l;
③函数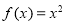 不是回
不是回 旋函数;
旋函数;
④若f(x)是t=2的回旋函数,则f(x)在[0,4030]上至少有2015个零点.
其中为真命题的是_________(写出所有真命题的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com