
分析 画出函数$f(x)=\left\{{\begin{array}{l}{x(x+1),x≥0}\\{x(1-x),x<0}\end{array}}\right.$的图象,分析函数的单调性,结合f(t-1)<f(2t),可得实数t的取值范围.
解答 解:函数$f(x)=\left\{{\begin{array}{l}{x(x+1),x≥0}\\{x(1-x),x<0}\end{array}}\right.$的图象如下图所示: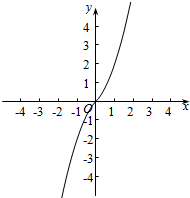
由图可得:函数f(x)在定义域R上为增函数,
若f(t-1)<f(2t),则t-1<2t,
解得:t>-1,
故答案为:t>-1
点评 本题考查的知识点是分段函数的应用,函数单调性的性质,难度不大,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 75,25 | B. | 75,16 | C. | 60,144 | D. | 60,16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=cos(2x-\frac{π}{3})$ | B. | $y=cos(2x-\frac{2π}{3})$ | C. | $y=cos(\frac{x}{2}-\frac{π}{3})$ | D. | $y=cos(\frac{x}{2}-\frac{π}{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com