
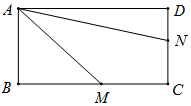
 如图,某地区有四个公司分别位于矩形ABCD的四个顶点,且AB=1km,BC=2km,四个公司商量准备在矩形空地中规划一个三角形区域AMN种植花草,其中M,N分别在直线BC,CD上运动,∠MAN=30°,设∠BAM=α,当三角AMN的面积最小时,此时α=( )
如图,某地区有四个公司分别位于矩形ABCD的四个顶点,且AB=1km,BC=2km,四个公司商量准备在矩形空地中规划一个三角形区域AMN种植花草,其中M,N分别在直线BC,CD上运动,∠MAN=30°,设∠BAM=α,当三角AMN的面积最小时,此时α=( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{5π}{12}$ |
分析 由已知可求AM=$\frac{1}{cosα}$,AN=$\frac{2}{cos(\frac{π}{3}-α)}$,可求三角形面积,利用三角函数的恒等变换化简得到S△AMN关于α的三角函数,利用正弦函数的性质结合α的范围即可计算得解.
解答 解:由于:∠BAM=α,
由题意可知,AM=$\frac{1}{cosα}$,AN=$\frac{2}{cos(\frac{π}{3}-α)}$,
则S△AMN=$\frac{1}{2}$AM•ANsin$\frac{π}{6}$=$\frac{1}{2}×$$\frac{1}{cosα}$×$\frac{2}{cos(\frac{π}{3}-α)}$=$\frac{1}{\frac{1}{2}co{s}^{2}α+\frac{\sqrt{3}}{2}sinαcosα}$=$\frac{1}{\frac{1}{2}(\frac{1}{2}cos2α+\frac{\sqrt{3}}{2}sin2α)+\frac{1}{4}}$
=$\frac{4}{2sin(2α+\frac{π}{6})+1}$,
当$α=\frac{π}{6}$时,三角形AMN面积最小.
故选:B.
点评 本题考查了三角函数的恒等变换,三角形的面积公式,考查了转化思想和数形结合思想的应用,属于中档题.


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{9}$ | B. | -9 | C. | $\frac{1}{9}$ | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\frac{5}{4}$ | B. | ±$\frac{4}{3}$ | C. | ±$\frac{4}{5}$ | D. | ±$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,2) | C. | (1,0) | D. | (2,0) (第4题图) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com