
分析 (Ⅰ)求出函数f(x)的解析式,求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(Ⅱ)求出f′(x),令F(x)=f(a)+f(x)-2f($\frac{a+x}{2}$),求出F′(x),利用函数的单调性求出当x=a时,F(x)的最小值0,再根据b>a,即可确定F(b)>F(a),从而证得f(a)+f(b)-2f($\frac{a+b}{2}$)>0,得到$\frac{f(a)+f(b)}{2}$与$f(\frac{a+b}{2})$的大小即可.
解答 解:f′(x)=mlnx+m+$\frac{n}{x}$,(x>0),
故f(e)=me+n,f′(e)=2m+$\frac{n}{e}$,
故切线方程是:y=(2m+$\frac{n}{e}$)x-me=2x-e,
故m=1,n=0,
故f(x)=xlnx;
(Ⅰ)∵f(x)的定义域是(0,+∞),
f′(x)=1+lnx,
令f′(x)>0,解得:x>$\frac{1}{e}$,
令f′(x)<0,解得:0<x<$\frac{1}{e}$,
故f(x)在(0,$\frac{1}{e}$)递减,在($\frac{1}{e}$,+∞);
(Ⅱ)不妨设0<a≤b,∵f(x)=xlnx,
∴f'(x)=lnx+1,
令F(x)=f(a)+f(x)-2f($\frac{a+x}{2}$),
∴F′(x)=f′(x)-f′($\frac{a+x}{2}$)=lnx-ln$\frac{a+x}{2}$,
当0<x<a时,F'(x)<0,当a<x时,F'(x)>0,
∴F(x)在(0,a)上为减函数,F(x)在(a,+∞)上为增函数,
∴当x=a时,F(x)min=F(a)=0,
∵b≥a,
∴F(b)>F(a),
∴f(a)+f(b)-2f($\frac{a+b}{2}$)>0,
∴$\frac{f(a)+f(b)}{2}$>$f(\frac{a+b}{2})$.
点评 本题考查了利用导数研究函数的单调性,对于利用导数研究函数的单调性,注意导数的正负对应着函数的单调性.利用导数研究函数问题时,经常会运用分类讨论的数学思想方法.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}+\frac{y^2}{3}$=1 | B. | $\frac{x^2}{16}+\frac{y^2}{12}=1$ | C. | $\frac{x^2}{4}+{y^2}=1$ | D. | $\frac{x^2}{16}+\frac{y^2}{4}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
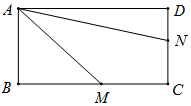 如图,某地区有四个公司分别位于矩形ABCD的四个顶点,且AB=1km,BC=2km,四个公司商量准备在矩形空地中规划一个三角形区域AMN种植花草,其中M,N分别在直线BC,CD上运动,∠MAN=30°,设∠BAM=α,当三角AMN的面积最小时,此时α=( )
如图,某地区有四个公司分别位于矩形ABCD的四个顶点,且AB=1km,BC=2km,四个公司商量准备在矩形空地中规划一个三角形区域AMN种植花草,其中M,N分别在直线BC,CD上运动,∠MAN=30°,设∠BAM=α,当三角AMN的面积最小时,此时α=( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{π}$ | B. | $\frac{{\sqrt{π}}}{2π}$ | C. | $-\sqrt{π}$ | D. | $\frac{{\sqrt{2π}}}{2π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | -3 | C. | 3 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,$\overrightarrow{BF}=2\overrightarrow{FC}$,$\overrightarrow{AM}=\overrightarrow{MF}=\overrightarrow{FN}$.
如图,在△ABC中,$\overrightarrow{BF}=2\overrightarrow{FC}$,$\overrightarrow{AM}=\overrightarrow{MF}=\overrightarrow{FN}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com