
| A. | ±$\frac{5}{4}$ | B. | ±$\frac{4}{3}$ | C. | ±$\frac{4}{5}$ | D. | ±$\frac{3}{4}$ |
分析 求出椭圆的半焦距,得到双曲线的实半轴的长,然后求解b,得到双曲线方程,求出双曲线的渐近线方程,即可得到斜率.
解答 解:椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1中半焦距为:$\sqrt{25-9}$=4,从而双曲线的半实轴长为:4,半焦距为:5,所以b2=25-16=9,所以双曲线方程为:$\frac{{x}^{2}}{16}-\frac{{y}^{2}}{9}=1$,从而其渐近线方程为:y=$±\frac{3}{4}x$,所以双曲线的渐近线的斜率为:$±\frac{3}{4}$,
故选:D.
点评 本题考查椭圆的简单性质与双曲线的简单性质的应用,考查计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
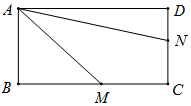 如图,某地区有四个公司分别位于矩形ABCD的四个顶点,且AB=1km,BC=2km,四个公司商量准备在矩形空地中规划一个三角形区域AMN种植花草,其中M,N分别在直线BC,CD上运动,∠MAN=30°,设∠BAM=α,当三角AMN的面积最小时,此时α=( )
如图,某地区有四个公司分别位于矩形ABCD的四个顶点,且AB=1km,BC=2km,四个公司商量准备在矩形空地中规划一个三角形区域AMN种植花草,其中M,N分别在直线BC,CD上运动,∠MAN=30°,设∠BAM=α,当三角AMN的面积最小时,此时α=( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -144 | B. | -120 | C. | -80 | D. | -60 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | -3 | C. | 3 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com