
在数列{an}中,a1=1,an+1=2an+2n.
(1)设bn=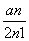 .证明:数列{bn}是等差数列;
.证明:数列{bn}是等差数列;
(2)求数列{an}的前n项和.
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
“嫦娥奔月,举国欢庆”,据科学计算,运载“神六”的“长征二号”系列火箭,在点火第一秒钟通过的路程为2 km,以后每秒钟通过的路程都增加2 km,在达到离地面240 km的高度时,火箭与飞船分离,则这一过程大约需要的时间是________秒.
查看答案和解析>>
科目:高中数学 来源: 题型:
设a>1,b>1且ab-(a+b)=1,那么( )
A.a+b有最小值2(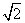 +1)
+1)
B.a+b有最大值(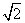 +1)2
+1)2
C.ab有最大值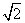 +1
+1
D.ab有最小值2(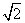 +1)
+1)
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙两人同时从寝室到教室,甲一半路程步行,一半路程跑步,乙一半时间步行,一半时间跑步,如果两人步行速度、跑步速度均相同,则( )
A.甲先到教室 B.乙先到教室
C.两人同时到教室 D.谁先到教室不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com