
 某中学从高三甲、乙两个班中各选出7名学生参加数学竞赛,他们取得的成绩如下:
某中学从高三甲、乙两个班中各选出7名学生参加数学竞赛,他们取得的成绩如下:分析 (Ⅰ)先列举出所有的基本事件,再找到满足条件的基本事件,根据概率公式计算即可.
(Ⅱ)画出茎叶图,根据众数和中位数的概念求出甲班学生成绩的众数,乙班学生成绩中位数,再求出平均数、方差,分析即可.
解答 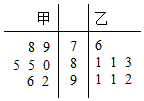 解:(Ⅰ)乙班有四名学生成绩为优秀,设为a1,a2,a3,甲班有两名学生成绩为优秀,设为b1,b2,
解:(Ⅰ)乙班有四名学生成绩为优秀,设为a1,a2,a3,甲班有两名学生成绩为优秀,设为b1,b2,
则选取两名成绩为优秀的学生的所有可能为:(a1,a2),(a1,a3),(a1,b1),(a1,b2),(a2,a3),(a2,b1),(a2,b2),(a3,b1),(a3,b2),(b1,b2)共10种可能,
其中乙班恰好只有1名的有6种可能,
故乙班恰好只有1名的概率是概率P=$\frac{6}{10}$=$\frac{3}{5}$;
(Ⅱ)茎叶图如图.
甲班学生成绩的众数85,乙班学生成绩中位数83,
$\overline{{X}_{甲}}$=$\frac{1}{7}$(78+79+80+85+85+92+96)=85,$\overline{{X}_{乙}}$=$\frac{1}{7}$(76+81+81+83+91+91+92)=85,
${S}_{甲}^{2}$=$\frac{1}{7}$[(78-85)2+(79-85)2+(80-85)2+(85-85)2+(85-85)2+(92-85)2+(96-85)2]=40
${S}_{乙}^{2}$=$\frac{1}{7}$[(76-85)2+(81-85)2+(81-85)2+(83-85)2+(91-85)2+(91-85)2+(92-85)2]=34
统计结论甲班的平均成绩等于乙班的平均成绩;
②乙班的成绩比甲班的成绩更稳定.
点评 本题考查数据的平均数公式、方差与茎叶图,古典概率,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 大量的试验中,出现正面的频率稳定于$\frac{1}{2}$ | |
| B. | 不管试验多少次,出现正面的概率始终为$\frac{1}{2}$ | |
| C. | 试验次数增多,出现正面的经验概率越接近$\frac{1}{2}$ | |
| D. | 试验次数无限增大时,出现正面的频率的极限为$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
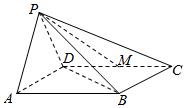 如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.
如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com