
分析 (1)当n=3、2和1,分别求得a3=11,a2=6和a1a1=3,猜想${a}_{n}=n+{2}^{n}$;
(2)根据数列{an}的通项公式,写出前n项和公式,$\frac{{n}^{2}+n}{2}$+2n+1-2>2016,解得n的取值范围.
解答 解:当n=3时,a4=2a3-3+1=20,a3=11,
当n=2时,a3=2a2-2+1=11,a2=6,
当n=1时,a2=2a1-1+1=6,a1=3;
猜想${a}_{n}=n+{2}^{n}$(n∈N*)
(2)由(1)得${a}_{n}=n+{2}^{n}$,a1=3,
Sn=a1+a2+a3+…+an,
=(1+2)+(2+22)+(3+23)+…+(n+2n),
=(1+2+3+…+n)+(2+22+23+…+2n),
=$\frac{{n}^{2}+n}{2}$+2n+1-2,
∵Sn>2016,$\frac{{n}^{2}+n}{2}$+2n+1-2>2016,
∴n≥10,
n的最小值为10.
点评 本题考查了数列递推公式的应用,根据前n项猜想写出通项公式及等比和等差数列的前n项和,属于中档题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
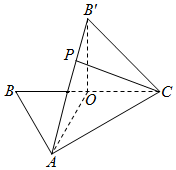 如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2,将△BAO沿AO折起,使B点到达B′点.
如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2,将△BAO沿AO折起,使B点到达B′点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某中学从高三甲、乙两个班中各选出7名学生参加数学竞赛,他们取得的成绩如下:
某中学从高三甲、乙两个班中各选出7名学生参加数学竞赛,他们取得的成绩如下:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=2sin(x+$\frac{π}{6}$) | B. | f(x)=2sin(2x+$\frac{2π}{3}$) | C. | f(x)=2sin(x+$\frac{π}{3}$) | D. | f(x)=2sin(2x+$\frac{5π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x<2} | B. | {x|-3<x<2} | C. | {x|-6<x<0} | D. | {x|x≥0} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com