
【题目】已知以点 ![]() 为圆心的圆与直线
为圆心的圆与直线 ![]() 相切,过点
相切,过点 ![]() 的动直线与圆
的动直线与圆 ![]() 相交于
相交于 ![]() 两点.
两点.
(1)求圆 ![]() 的方程;
的方程;
(2)当 ![]() 时,求直线
时,求直线 ![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】某商场在一部向下运行的手扶电梯终点的正上方竖直悬挂一幅广告画.如图,该电梯的高AB为4米,它所占水平地面的长AC为8米.该广告画最高点E到地面的距离为10.5米.最低点D到地面的距离6.5米.假设某人的眼睛到脚底的距离MN为1.5米,他竖直站在此电梯上观看DE的视角为θ. 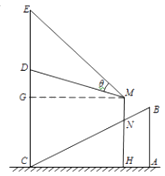
(1)设此人到直线EC的距离为x米,试用x表示点M到地面的距离;
(2)此人到直线EC的距离为多少米,视角θ最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的最下正周期为π,且点P(
)的最下正周期为π,且点P( ![]() ,2)是该函数图象的一个人最高点.
,2)是该函数图象的一个人最高点.
(1)求函数f(x)的解析式;
(2)若x∈[﹣ ![]() ,0],求函数y=f(x)的值域;
,0],求函数y=f(x)的值域;
(3)把函数y=f(x)的图线向右平移θ(0<θ< ![]() )个单位,得到函数y=g(x)在[0,
)个单位,得到函数y=g(x)在[0, ![]() ]上是单调增函数,求θ的取值范围.
]上是单调增函数,求θ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知向量 ![]() ,
, ![]() ,定点
,定点 ![]() 的坐标为
的坐标为 ![]() ,点
,点 ![]() 满足
满足 ![]() ,曲线
,曲线 ![]() ,区域
,区域 ![]() ,曲线
,曲线 ![]() 与区域
与区域 ![]() 的交集为两段分离的曲线,则( )
的交集为两段分离的曲线,则( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】葫芦岛市某高中进行一项调查:2012年至2016年本校学生人均年求学花销 ![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
年求学花销 | 3.2 | 3.5 | 3.8 | 4.6 | 4.9 |
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
(1)求 ![]() 关于
关于 ![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2012年至2016年本校学生人均年求学花销的变化情况,并预测该地区2017年本校学生人均年求学花销情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位实行休年假制度三年以来,50名职工休年假的次数进行的调查统计结果如表所示:
根据下表信息解答以下问题:
休假次数 | 0 | 1 | 2 | 3 |
人数 | 5 | 10 | 20 | 15 |
(1)从该单位任选两名职工,用η表示这两人休年假次数之和,记“函数f(x)=x2﹣ηx﹣1在区间(4,6)上有且只有一个零点”为事件A,求事件A发生的概率P;
(2)从该单位任选两名职工,用ξ表示这两人休年假次数之差的绝对值,求随机变量ξ的分布列及数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C的对边分别为a,b,c,满足2asinA=(2b﹣ ![]() c)sinB+(2c﹣
c)sinB+(2c﹣ ![]() b)sinC. (Ⅰ)求角A的大小;
b)sinC. (Ⅰ)求角A的大小;
(Ⅱ)若a=2,b=2 ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在班级的演讲比赛中,将甲、乙两名同学的得分情况制成如图所示的茎叶图.记甲、乙两名同学所得分数的平均分分别为 ![]() 甲、
甲、 ![]() 乙 , 则下列判断正确的是( )
乙 , 则下列判断正确的是( ) 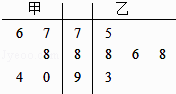
A.![]() 甲<
甲< ![]() 乙 , 甲比乙成绩稳定
乙 , 甲比乙成绩稳定
B.![]() 甲>
甲> ![]() 乙,甲比乙成绩稳定
乙,甲比乙成绩稳定
C.![]() 甲<
甲< ![]() 乙 , 乙比甲成绩稳定
乙 , 乙比甲成绩稳定
D.![]() 甲>
甲> ![]() 乙 , 乙比甲成绩稳定
乙 , 乙比甲成绩稳定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com