
分析 求出p、q为真时,对应a的取值范围,再根据复合命题的真假性得出p,q的真假性,从而求出a的取值范围.
解答 解:若p为真,则a=0或$\left\{\begin{array}{l}{a>0}\\{△{=a}^{2}-4a<0}\end{array}\right.$,
解得0<a<4;
当命题p为真时,a的范围是:0≤a<4;
若q为真,则△=1-4a≥0,解得a≤$\frac{1}{4}$;
又p∧q为假命题,p∨q为真命题,
故p,q必一真一假;
①、若p真q假时,$\left\{\begin{array}{l}{a>\frac{1}{4}}\\{0≤a<4}\end{array}\right.$,
解得$\frac{1}{4}$<a<4;
②、若p假q真时,$\left\{\begin{array}{l}{a≥4或a<0}\\{a≤\frac{1}{4}}\end{array}\right.$,
解得a<0;
综上所述,所求a的范围是:(-∞,0)∪($\frac{1}{4}$,4).
点评 本题考查了复合命题真假性的应用问题,是综合性题目.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {1,2} | C. | {0,1,2} | D. | {2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
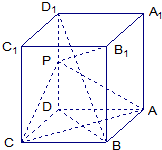 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.求:
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{8}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
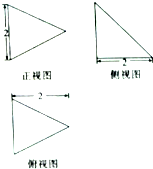
| A. | $2\sqrt{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com