
【题目】如图,在直三棱柱![]() 中,
中,![]() 分别是棱
分别是棱![]() 上的点(点
上的点(点![]() 不同于点
不同于点![]() ),且
),且![]() ,
,![]() 为棱
为棱![]() 上的点,且
上的点,且![]() .
.
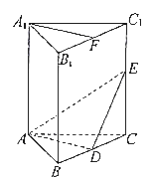
求证:(1)平面![]() 平面
平面![]() ;
;
(2)![]() 平面
平面![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)推导出BB1⊥AD,AD⊥DE,从而AD⊥平面BCC1B1,由此能证明平面ADE⊥平面BCC1B1.(2)推导出BB1⊥平面A1B1C1,BB1⊥A1F,A1F⊥B1C1,从而A1F⊥平面BCC1B1,再由AD⊥平面BCC1B1,得A1F∥AD,由此能证明A1F∥平面ADE.
(1)在直三棱柱ABC﹣A1B1C1中,BB1⊥平面ABC,因为AD平面ABC,所以BB1⊥AD,
又因为AD⊥DE,在平面BCC1B1中,BB1与DE相交,
所以AD⊥平面BCC1B1,
又因为AD平面ADE,所以平面ADE⊥平面BCC1B1.
(2)在直三棱柱ABC﹣A1B1C1中,BB1⊥平面A1B1C1,
因为A1F平面A1B1C1,所以BB1⊥A1F,
又因为A1F⊥B1C1,
在平面BCC1B1中,BB1∩B1C1=B1,
所以A1F⊥平面BCC1B1,
在(1)中已证得AD⊥平面BCC1B1,
所以A1F∥AD,又因为A1F平面ADE,AD![]() 平面ADE,
平面ADE,
所以A1F∥平面ADE.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】由无理数论引发的数字危机一直延续到19世纪,直到1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机,所谓戴德金分割,是指将有理数集![]() 划分为两个非空的子集
划分为两个非空的子集![]() 与
与![]() ,且满足
,且满足![]() ,
,![]() ,
,![]() 中的每一个元素都小于
中的每一个元素都小于![]() 中的每一个元素,则称
中的每一个元素,则称![]() 为戴德金分割.试判断,对于任一戴德金分割
为戴德金分割.试判断,对于任一戴德金分割![]() ,下列选项中,可能成立的是____.
,下列选项中,可能成立的是____.
①![]() 没有最大元素,
没有最大元素,![]() 有一个最小元素;②
有一个最小元素;②![]() 没有最大元素,
没有最大元素,![]() 也没有最小元素;
也没有最小元素;
③![]() 有一个最大元素,
有一个最大元素,![]() 有一个最小元素;④
有一个最小元素;④![]() 有一个最大元素,
有一个最大元素,![]() 没有最小元素.
没有最小元素.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆:![]() 的四个顶点围成的四边形的面积为
的四个顶点围成的四边形的面积为![]() ,原点到直线
,原点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知定点![]() ,是否存在过
,是否存在过![]() 的直线
的直线![]() ,使
,使![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 的左顶点?若存在,求出
的左顶点?若存在,求出![]() 的方程:若不存在,请说明理由.
的方程:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,一条准线方程为
,一条准线方程为![]()
⑴求椭圆![]() 的方程;
的方程;
⑵设![]() 为椭圆
为椭圆![]() 上的两个动点,
上的两个动点,![]() 为坐标原点,且
为坐标原点,且![]() .
.
①当直线![]() 的倾斜角为
的倾斜角为![]() 时,求
时,求![]() 的面积;
的面积;
②是否存在以原点![]() 为圆心的定圆,使得该定圆始终与直线
为圆心的定圆,使得该定圆始终与直线![]() 相切?若存在,请求出该定圆方程;若不存在,请说明理由.
相切?若存在,请求出该定圆方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有如下三个命题:
甲:相交直线l、m都在平面![]() 内,并且都不在平面
内,并且都不在平面![]() 内;
内;
乙:直线l、m中至少有一条与平面![]() 相交;
相交;
丙:平面![]() 与平面
与平面![]() 相交.
相交.
当甲成立时![]()
![]()
A. 乙是丙的充分而不必要条件
B. 乙是丙的必要而不充分条件
C. 乙是丙的充分且必要条件
D. 乙既不是丙的充分条件又不是丙的必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,该椭圆经过点
,该椭圆经过点![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 是圆
是圆![]() 上任意一点,由
上任意一点,由![]() 引椭圆
引椭圆![]() 的两条切线
的两条切线![]() ,
,![]() ,当两条切线的斜率都存在时,证明:两条切线斜率的积为定值.
,当两条切线的斜率都存在时,证明:两条切线斜率的积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班进行了![]() 次数学测试,其中甲、乙两人的成绩统计情况如茎叶图所示:
次数学测试,其中甲、乙两人的成绩统计情况如茎叶图所示:
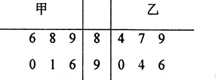
(I)该班数学老师决定从甲、乙两人中选派一人去参加数学比赛,你认为谁去更合适?并说明理由;
(II)从甲的成绩中人去两次作进一步的分析,在抽取的两次成绩中,求至少有一次成绩在![]() 之间的概率.
之间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com