练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．用1、2、3、4、5、6、7这7个数字组成没有重复数字的数．
    （1）这些四位数中偶数有多少个？能被5整除的有多少个？
    （2）这些四位数中大于6500的有多少个？

    分析 （1）先排个位，再确定前三位，由分步乘法计数原理可得结论；能被5整除的数个位必须是5，从而可求能被5整除的四位数；
    （2）分类完成：最高位上是6时，百位上只能是7或5；最高位是7时，即可得到结论．

    解答 解：（1）偶数的个位数只能是2、4、6、8有共4种排法，其它位上任意排，由分步乘法计数原理知共有四位偶数4A63=480个；
    能被5整除的数个位必须是5，故有A63=120个；
    （2）最高位上是6时，百位上只能是7或5，共有2种，其它任意排，故有2A52=40个，
    最高位是7时，共A63=120个
    ∴由分类加法计数原理知，这些四位数中大于6500的共有40+120=160．

    点评 本题考查排列知识，考查学生分析解决问题的能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    7．曲线y=$\frac{sinx}{x}$在点M（2π，0）处的切线方程为x-2πy-2π=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．若直线y=$\frac{1}{3}$x+b是曲线y=lnx（x＞0）的一条切线，则实数b的值是ln3-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．某学校准备从4名男同学和2名女同学中选出2人代表学校参加数学竞赛，则至少一名女同学被选中的概率是$\frac{3}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．函数y=x2-1的图象上一点（1，0）处的切线的斜率为（　　）
    A．1B．2C．0D．-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

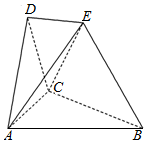    2．在如图所示的空间几何体中，平面ACD⊥平面ABC，△ACD与△ACB是边长为2的等边三角形，BE=2，BE和平面ABC所成角为60°，且点E在平面ABC上射影落在∠ABC的平分线上．
    （1）求证：DE∥平面ABC
    （2）求此空间几何体的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

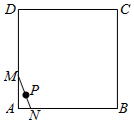    9．如图所示，有一条长度为1的线段MN，其端点M，N在边长为3的正方形ABCD的四边上滑动，当点N绕着正方形的四边滑动一周时，MN的中点P所形成轨迹的长度为（　　）
    A．$8+\frac{π}{2}$B．8+πC．$12+\frac{π}{2}$D．12+π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．在一次围棋比赛中，共有24人参加，现今成6组，每组进行单循环赛，每组的第一名共6人，再分成2组进行单循环赛，两组的第一名决冠亚军，一共进行了多少场比赛？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（{a＞b＞0}），F1，F2是左右焦点，A，B是长轴两端点，点P（a，b）与F1，F2围成等腰三角形，且${S_{△P{F_1}{F_2}}}$=$\sqrt{3}$．
    （I）求椭圆C的方程；
    （Ⅱ）设点Q是椭圆上异于A，B的动点，直线x=-4与QA，QB分别交于M，N两点．
    （i）当$\overrightarrow{Q{F_1}}$=λ$\overrightarrow{MN}$时，求Q点坐标；
    （ii）过点M，N，F1三点的圆是否经过x轴上不同于点F1的定点？若经过，求出定点坐标，若不经过，请说明理由．

    查看答案和解析>>

    同步练习册答案