
分析 (1)设出圆的一般方程,利用待定系数法列出方程组,即可求出圆的方程;
(2)设出点A、B以及AB的中点M的坐标,由方程组$\left\{\begin{array}{l}{{(x-4)}^{2}{+(y+3)}^{2}=25}\\{x-y+m=0}\end{array}\right.$和中点坐标公式求出点M的坐标,代入圆的方程x2+y2=5中,即可求出m的值.
解答 解:(1)设过点O、M1和M2圆的方程为x2+y2+Dx+Ey+F=0,
则$\left\{\begin{array}{l}{F=0}\\{2+D+E+F=0}\\{20+4D+2E+F=0}\end{array}\right.$,
解得D=-8,E=6,F=0;
所求圆的方程为x2+y2-8x+6y=0,
化为标准方程是:(x-4)2+(y+3)2=25;
(2)设点A(x1,y1),B(x2,y2),AB的中点M(x0,y0),
由方程组$\left\{\begin{array}{l}{{(x-4)}^{2}{+(y+3)}^{2}=25}\\{x-y+m=0}\end{array}\right.$,消去y得2x2+2(m-1)x+m2+6m=0,
所以x0=$\frac{{x}_{1}{+x}_{2}}{2}$=$\frac{1-m}{2}$,y0=x0+m=$\frac{1+m}{2}$,
因为点M在圆上,所以${{x}_{0}}^{2}$+${{y}_{0}}^{2}$=5,
所以${(\frac{1-m}{2})}^{2}$+${(\frac{1+m}{2})}^{2}$=5,
解得m=±3;
又△=4(m-1)2-4•2(m2+6m)>0,
解得-7-5$\sqrt{2}$<m<-7+5$\sqrt{2}$,
综上,m=-3.
点评 本题考查了待定系数法求圆的方程的应用问题,也考查了函数与方程思想的合理运用问题,是综合题.


科目:高中数学 来源: 题型:解答题
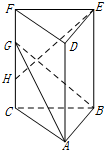 如图所示,在直三棱柱ABC-DEF中,底面ABC的棱AB⊥BC,且AB=BC=2.点G、H在棱CF上,且GH=HG=GF=1
如图所示,在直三棱柱ABC-DEF中,底面ABC的棱AB⊥BC,且AB=BC=2.点G、H在棱CF上,且GH=HG=GF=1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直线AB经过⊙O上一点C,⊙O的半径为3,△AOB是等腰三角形,且C是AB中点,⊙O交直线OB于E、D.
如图,直线AB经过⊙O上一点C,⊙O的半径为3,△AOB是等腰三角形,且C是AB中点,⊙O交直线OB于E、D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,正方体AC1的棱长为a,MN分别为BC1和AC上的点,且$\overrightarrow{AN}$=2$\overrightarrow{NC}$,$\overrightarrow{BM}$=2$\overrightarrow{M{C}_{1}}$,则MN的长为( )
如图,正方体AC1的棱长为a,MN分别为BC1和AC上的点,且$\overrightarrow{AN}$=2$\overrightarrow{NC}$,$\overrightarrow{BM}$=2$\overrightarrow{M{C}_{1}}$,则MN的长为( )| A. | a | B. | $\sqrt{2}$a | C. | $\frac{\sqrt{5}}{3}$a | D. | $\frac{\sqrt{6}}{3}$a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x+1 | B. | y=log3x | C. | y=$(\frac{1}{3})^{x}$ | D. | y=${x}^{\frac{1}{3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com