
分析 根据题意,由已知命题,类比另一命题时,应结合命题的结构形式和推理方法进行类比,即可得出结论tanαtanβ+tanαtanγ+tanβtanγ=1.
解答 解:斜△ABC中,由A+B+C=π,得A+B=π-C,
则tan(A+B)=tan(π-C),
化简得tanA+tanB+tanC=tanAtanBtanC;
类比上述方法,
正角α,β,γ满足α+β+γ=$\frac{π}{2}$,得α+β=$\frac{π}{2}$-γ,
则tan(α+β)=tan($\frac{π}{2}$-γ),
即$\frac{tanα+tanβ}{1-tanαtanβ}$=$\frac{1}{tanγ}$,
所以tanα,tanβ,tanγ满足的结论为
tanαtanβ+tanαtanγ+tanβtanγ=1.
故答案为:tanαtanβ+tanαtanγ+tanβtanγ=1.
点评 本题主要考查了两角和的正切公式以及三角函数的恒等变换问题,考查了推理论证能力,化归与转化思想的应用问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
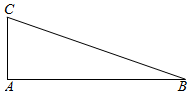 如图,在Rt△ABC中,∠CAB=90°,|AB|=2,|AC|=$\frac{\sqrt{2}}{2}$,一曲线E过点C,动点P在曲线E上运动,且保持|PA|+|PB|的值不变.
如图,在Rt△ABC中,∠CAB=90°,|AB|=2,|AC|=$\frac{\sqrt{2}}{2}$,一曲线E过点C,动点P在曲线E上运动,且保持|PA|+|PB|的值不变.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com