练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知f(x)＝xln x，若f′(x0)＝2，则x0＝(　　)．

    A．e2             B．e               C.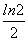             D．ln 2


    B解析　f(x)的定义域为(0，＋∞)，

    f′(x)＝ln x＋1，由f′(x0)＝2，

    即ln x0＋1＝2，解得x0＝e.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设函数f(x)＝2|x＋1|－|x－1|，求使f(x)≥2的x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    方程x2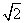＋x－1＝0的解可视为函数y＝x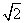＋的图象与函数y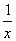＝的图象交点的横坐标，若x4＋ax－4＝0的各个实根x1，x2，…，xk(k≤4)所对应的点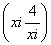(i＝1,2，…，k)均在直线y＝x的同侧，则实数a的取值范围是(　　)．

    A．R                                        B．∅ 

    C．(－6,6)                                  D．(－∞，－6)∪(6，＋∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某厂有许多形状为直角梯形的铁皮边角料，如图，为降低消耗，开源节流，现要从这些边角料上截取矩形铁片(如图中阴影部分)备用，当截取的矩形面积最大时，矩形两边长x、y应为(　　)．

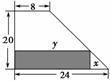
    A．x＝15，y＝12                                    B．x＝12，y＝15

    C．x＝14，y＝10                                    D．x＝10，y＝14

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某化工厂引进一条先进生产线生产某种化工产品，其生产的总成本y(万元)与年产量x(吨)之间的函数关系式可以近似地表示为y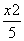＝－48x＋8 000，已知此生产线年产量最大为210吨．

    (1)求年产量为多少吨时，生产每吨产品的平均成本最低，并求最低成本；

    (2)若每吨产品平均出厂价为40万元，那么当年产量为多少吨时，可以获得最大利润？最大利润是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝f′sin x＋cos x，则f＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    求下列函数的导数．

    y＝log2(2x2＋3x＋1)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝ax2＋blnx在x＝1处有极值.

    (1)求a，b的值；

    (2)判断函数y＝f(x)的单调性并求出单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知角α的终边过点P(－8m，－6sin 30°)，且cos α＝－，则m的值为

    (　　)．　　　　　　　　　　　　　　　　　

    A．－           B.               C．－          D.

    查看答案和解析>>

    同步练习册答案