
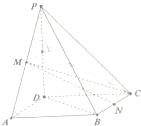
 如图,在四棱锥P-ABCD中,底面ABCD是矩形,M,N分别为PA、BC的中点,PD⊥平面ABCD,且PD=AD=$\sqrt{2}$,CD=1.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,M,N分别为PA、BC的中点,PD⊥平面ABCD,且PD=AD=$\sqrt{2}$,CD=1.分析 (1)首先以DA,DC,DP三直线分别为x,y,z轴,建立空间直角坐标系,写出图形中点的坐标,根据已知$\overrightarrow{DA}$为平面PCD的一条法向量,要证明MN∥平面PCD,只要证明$\overrightarrow{MN}⊥\overrightarrow{DA}$,即求$\overrightarrow{MN}•\overrightarrow{DA}=0$即可;
(2)求出$\overrightarrow{MC},\overrightarrow{BD}$的坐标,求$\overrightarrow{MC}•\overrightarrow{BD}=0$,从而得到$\overrightarrow{MC}⊥\overrightarrow{BD}$,这样便得出MC⊥BD;
(3)容易看出$\overrightarrow{DC}$为平面PAD的一条法向量,可设平面PBC的法向量为$\overrightarrow{n}=(x,y,z)$,由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PB}=0}\\{\overrightarrow{n}•\overrightarrow{PC}=0}\end{array}\right.$即可求出法向量$\overrightarrow{n}$.设平面PAD与平面PBC所成的锐二面角的大小为θ,从而根据cosθ=$|cos<\overrightarrow{DC},\overrightarrow{n}>|$即可求出cosθ,也就是求出了平面PAD与平面PBC所成的锐二面角的余弦值.
解答 解:根据已知,DA,DC,DP三直线两两垂直,分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系,则:
D(0,0,0),A($\sqrt{2}$,0,0),B($\sqrt{2}$,1,0),C(0,1,0),P(0,0,$\sqrt{2}$),M($\frac{\sqrt{2}}{2},0,\frac{\sqrt{2}}{2}$),N($\frac{\sqrt{2}}{2},1,0$);
(1)证明:$\overrightarrow{DA}=(\sqrt{2},0,0)$为平面PCD的一条法向量,$\overrightarrow{MN}=(0,1,-\frac{\sqrt{2}}{2})$;
∴$\overrightarrow{MN}•\overrightarrow{DA}=0$;
∴$\overrightarrow{MN}⊥\overrightarrow{DA}$;
∴MN∥平面PCD;
(2)证明:$\overrightarrow{MC}$=($-\frac{\sqrt{2}}{2},1,-\frac{\sqrt{2}}{2}$),$\overrightarrow{BD}=(-\sqrt{2},-1,0)$;
∴$\overrightarrow{MC}•\overrightarrow{BD}=1-1+0=0$;
∴$\overrightarrow{MC}⊥\overrightarrow{BD}$;
∴MC⊥BD;
(3)$\overrightarrow{DC}=(0,1,0)$为平面PAD的一条法向量,$\overrightarrow{PB}=(\sqrt{2},1,-\sqrt{2})$,$\overrightarrow{PC}=(0,1,-\sqrt{2})$;
设平面PBC的法向量为$\overrightarrow{n}=(x,y,z)$,则:
$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PB}=\sqrt{2}x+y-\sqrt{2}z=0}\\{\overrightarrow{n}•\overrightarrow{PC}=y-\sqrt{2}z=0}\end{array}\right.$;
∴$\left\{\begin{array}{l}{x=0}\\{y=\sqrt{2}z}\end{array}\right.$,取z=1,∴$\overrightarrow{n}=(0,\sqrt{2},1)$;
设平面PAD与平面PBC所成的锐二面角的大小为θ,则:
cosθ=|cos$<\overrightarrow{DC},\overrightarrow{n}>$|=$\frac{\sqrt{2}}{\sqrt{3}•1}=\frac{\sqrt{6}}{3}$;
∴平面PAD与平面PBC所成的锐二面角的余弦值为$\frac{\sqrt{6}}{3}$.
点评 考查建立空间直角坐标系,利用空间向量证明线面平行,线线垂直,以及求二面角的方法,线面垂直的性质,平面法向量的概念及求法,两非零向量垂直的充要条件,向量夹角余弦的坐标公式.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 在△ABC中,角A,B所对边分别为a,b则sinA>sinB成立的充要条件是a>b | |||||||||
| B. | 若命题p:?x∈(0,+∞),sinx-x<0,命题q:?x0∈(0,+∞),e${\;}^{{x}_{0}}$<0,则p∧¬q为真命题 | |||||||||
| C. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,则存在唯一的实数λ,使$\overrightarrow{a}$=λ$\overrightarrow{b}$ | |||||||||
| D. | 在一个2×2列联表中,由计算得k2=6.721,则有99%的把握确认这两个变量间有关系;可以参考独立性检验临界表
|
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
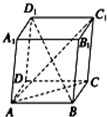 如图,平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长都相等,且它们彼此的夹角都是60°;记AC1=λAB,则λ的值为( )
如图,平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长都相等,且它们彼此的夹角都是60°;记AC1=λAB,则λ的值为( )| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | 2+$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com