
| A. | 在△ABC中,角A,B所对边分别为a,b则sinA>sinB成立的充要条件是a>b | |||||||||
| B. | 若命题p:?x∈(0,+∞),sinx-x<0,命题q:?x0∈(0,+∞),e${\;}^{{x}_{0}}$<0,则p∧¬q为真命题 | |||||||||
| C. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,则存在唯一的实数λ,使$\overrightarrow{a}$=λ$\overrightarrow{b}$ | |||||||||
| D. | 在一个2×2列联表中,由计算得k2=6.721,则有99%的把握确认这两个变量间有关系;可以参考独立性检验临界表
|
分析 根据正弦定理的推论(边角互化)可判断A;根据复合命题真假判断的真值表,可判断B;根据向量共线的充要条件,可判断C;根据独立性检验的方法可判断D.
解答 解:在△ABC中,A<B?a<b?2RsinA<2RsinB?sinA<sinB,即“A<B”是“sinA<sinB”成立的充要条件,∴A为真命题.
当x∈(0,+∞)时,令y=sinx-x,则y′=cosx-1≤0恒成立,故y=sinx-x在(0,+∞)上为减函数,故y|x=0=0,故命题p:?x∈(0,+∞),sinx-x<0,正确;
当x0∈(0,+∞),e${\;}^{{x}_{0}}$>0恒成立,故命题q:?x0∈(0,+∞),e${\;}^{{x}_{0}}$<0,错误;
则p∧¬q为真命题,
若$\overrightarrow{a}$=$\overrightarrow{b}$=$\overrightarrow{0}$时,$\overrightarrow{a}$∥$\overrightarrow{b}$,对实数λ,均使$\overrightarrow{a}$=λ$\overrightarrow{b}$,故C为假命题;
在一个2×2列联表中,由计算得k2=6.721>6.535,则有99%的把握确认这两个变量间有关系;故D为真命题;
故选:C.
点评 本题以命题的真假判断为载体考查了正弦定理,全称命题与特称命题,向量共线,独立性检验等知识点,难度中档.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:选择题
| A. | x-y=0 | B. | x+y=0 | C. | x-7y=0 | D. | x+7y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a-b<c | B. | a<b-c | C. | a<b<c | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
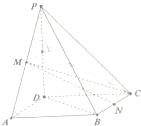 如图,在四棱锥P-ABCD中,底面ABCD是矩形,M,N分别为PA、BC的中点,PD⊥平面ABCD,且PD=AD=$\sqrt{2}$,CD=1.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,M,N分别为PA、BC的中点,PD⊥平面ABCD,且PD=AD=$\sqrt{2}$,CD=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com