
 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°AB=PC=2,AP=BP=$\sqrt{2}$
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°AB=PC=2,AP=BP=$\sqrt{2}$分析 (Ⅰ)取AB的中点O,连接PO,CO,由已知及ABCD为菱形得到PO⊥AB,CO⊥AB.再由线面垂直的判定得到
AB⊥平面PCO,从而得到AB⊥PC;
(Ⅱ)通过解直角三角形求得PO⊥OC,又PO⊥AB,得到PO为四棱锥P-ABCD的高,求出底面菱形的面积,代入棱锥体积公式求得四棱锥P-ABCD的体积.
解答 (Ⅰ)证明:取AB的中点O,连接PO,CO.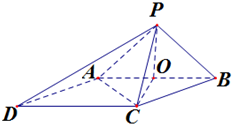 ∵AP=BP,∴PO⊥AB,
∵AP=BP,∴PO⊥AB,
又四边形ABCD是菱形,且∠BCD=120°,
∴△ACB是等边三角形,∴CO⊥AB.
又PO∩CO=O,
∴AB⊥平面PCO,又PC?平面PCO,∴AB⊥PC;
(Ⅱ)解:∵$PA=PB=\sqrt{2},AB=2$,
∴∠APB=90°,∴PO=1.
∵△ABC是边长为2的正三角形,
∴$OC=\sqrt{3}$,又PC=2,∴PO2+CO2=PC2,
∴PO⊥OC,又PO⊥AB,
∴PO为四棱锥P-ABCD的高,
∵∠BCD=120°,AB=2,
∴菱形ABCD的面积为$2×\frac{1}{2}×2×2sin120°=2\sqrt{3}$.
则所求棱锥体积为$\frac{1}{3}×2\sqrt{3}×1=\frac{2\sqrt{3}}{3}$.
点评 本题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,平行四边形ABCD中,AE,CF分别是∠BAD,∠BCD的平分线,根据现有的图形请添加一个条件,使四边形AECF是菱形,则添加的一个条件可以是AC⊥EF(只写出一个即可)
如图所示,平行四边形ABCD中,AE,CF分别是∠BAD,∠BCD的平分线,根据现有的图形请添加一个条件,使四边形AECF是菱形,则添加的一个条件可以是AC⊥EF(只写出一个即可)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
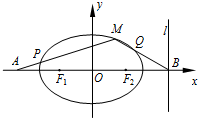 在平面直角坐标系xOy中,设中心在坐标原点的椭圆C的左、右焦点分别为F1、F2,右准线l:x=m+1与x轴的交点为B,BF2=m.
在平面直角坐标系xOy中,设中心在坐标原点的椭圆C的左、右焦点分别为F1、F2,右准线l:x=m+1与x轴的交点为B,BF2=m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图在以OA为半径的半圆M中,有三个半径为1的相同的半圆,在半圆M中任取一点N.
如图在以OA为半径的半圆M中,有三个半径为1的相同的半圆,在半圆M中任取一点N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
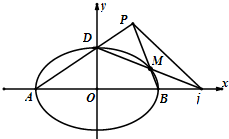 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,-2),且离心率为$\frac{{\sqrt{5}}}{3}$.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,-2),且离心率为$\frac{{\sqrt{5}}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com