Question

10．在钝角△ABC中，∠A为钝角，令$\overrightarrow{a}$=$\overrightarrow{AB}$，$\overrightarrow{b}$=$\overrightarrow{AC}$，若$\overrightarrow{AD}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$（x，y∈R）．现给出下面结论：
①当x=$\frac{1}{3}，y=\frac{1}{3}$时，点D是△ABC的重心；
②记△ABD，△ACD的面积分别为S_△ABD，S_△ACD，当x=$\frac{4}{5}，y=\frac{3}{5}$时，$\frac{{{S_{△ABD}}}}{{{S_{△ACD}}}}=\frac{3}{4}$；
③若点D在△ABC内部（不含边界），则$\frac{y+1}{x+2}$的取值范围是$（\frac{1}{3}，1）$；
④若$\overrightarrow{AD}$=λ$\overrightarrow{AE}$，其中点E在直线BC上，则当x=4，y=3时，λ=5．
其中正确的有①②③（写出所有正确结论的序号）．

Answer 1

分析 ①设BC的中点为M，判断$\overrightarrow{AD}$是否与$\frac{2}{3}\overrightarrow{AM}$相等即可；
②设$\overrightarrow{AP}=\frac{4}{5}\overrightarrow{a}$，$\overrightarrow{AQ}=\frac{3}{5}\overrightarrow{b}$，将△ABD，△ACD的面积转化为△APD，△AQD的面积来表示；
③求出x，y的范围，利用线性规划知识求出$\frac{y+1}{x+2}$的范围；
④用$\overrightarrow{a}，\overrightarrow{b}$表示出$\overrightarrow{AE}$，根据共线定理解出λ．

解答 解：①设BC的中点为M，则$\overrightarrow{AM}$=$\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$，
当x=y=$\frac{1}{3}$时，$\overrightarrow{AD}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$=$\frac{2}{3}\overrightarrow{AM}$，
∴D为AM靠近M的三等分点，故D为△ABC的重心．故①正确．
②设$\overrightarrow{AP}=\frac{4}{5}\overrightarrow{a}$，$\overrightarrow{AQ}=\frac{3}{5}\overrightarrow{b}$，则S_△APD=$\frac{4}{5}$S_△ABD，S_△AQD=$\frac{3}{5}$S_△ACD，
∵$\overrightarrow{AD}=\overrightarrow{AP}+\overrightarrow{AQ}$，∴S_△APD=S_△AQD，即$\frac{4}{5}$S_△ABD=$\frac{3}{5}$S_△ACD，
∴$\frac{{{S_{△ABD}}}}{{{S_{△ACD}}}}=\frac{3}{4}$，故②正确．
③∵D在△ABC的内部，∴$\left\{\begin{array}{l}{x＞0}\\{y＞0}\\{0＜x+y＜1}\end{array}\right.$，作出平面区域如图所示：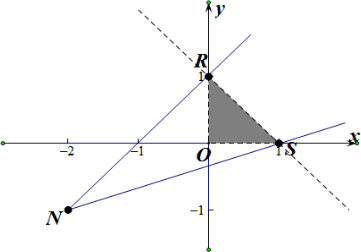

令$\frac{y+1}{x+2}$=k，则k为过点N（-2，-1）的点与平面区域内的点（x，y）的直线的斜率．
∴k的最小值为k_NS=$\frac{1}{3}$，最大值为k_NR=1．故③正确．
④当x=4，y=3时，$\overrightarrow{AD}=4\overrightarrow{a}+3\overrightarrow{b}$，
∵$\overrightarrow{AD}=λ\overrightarrow{AE}$，∴$\overrightarrow{AE}=\frac{1}{λ}\overrightarrow{AD}$=$\frac{4}{λ}\overrightarrow{a}+\frac{3}{λ}\overrightarrow{b}$，
∵E在BC上，∴$\frac{4}{λ}+\frac{3}{λ}$=1，λ=7，故④错误．
故答案为：①②③．

点评 本题考查了 平面向量的线性运算的几何意义，三角形重心的性质，线性规划等知识，属于中档题．