
| A. | 1 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{6}$ | D. | $-\frac{1}{6}$ |
分析 作出两个曲线的图象,求出它们的交点,由此可得所求面积为函数x-x2在区间[0,1]上的定积分的值,再用定积分计算公式加以计算,即可得到本题答案.
解答 解:∵曲线y=x3和曲线y=x的交点为A(1,1)和原点O(0,0)
∴由定积分的几何意义,可得所求图形的面积为
S=${∫}_{0}^{1}(x-{x}^{2})dx$=$(\frac{1}{2}{x}^{2}-\frac{1}{3}{x}^{3}){|}_{0}^{1}$=$\frac{1}{2}-\frac{1}{3}$=$\frac{1}{6}$.
故选:C.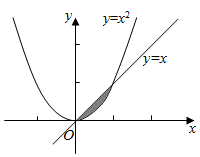
点评 本题求两条曲线围成的曲边图形的面积,着重考查了定积分的几何意义和积分计算公式等知识,属于基础题.


科目:高中数学 来源: 题型:解答题
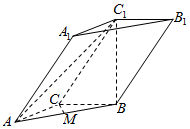 已知三棱柱ABC-A1B1C1的底面为等腰三角形,且平面B1BCC1⊥平面ABC,C1B⊥BC,M是线段AB上的点,且∠ACM=∠BCM=60°,CA=CB=$\frac{{\sqrt{3}}}{3}$C1B.
已知三棱柱ABC-A1B1C1的底面为等腰三角形,且平面B1BCC1⊥平面ABC,C1B⊥BC,M是线段AB上的点,且∠ACM=∠BCM=60°,CA=CB=$\frac{{\sqrt{3}}}{3}$C1B.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}i$ | B. | $\frac{1}{2}i$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1<a<1 | B. | a≤-$\frac{3}{5}$或a≥1 | C. | -1<a≤-$\frac{3}{5}$ | D. | -$\frac{3}{5}$≤a<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$-$\frac{i}{2}$ | B. | -$\frac{1}{2}$+$\frac{i}{2}$ | C. | $\frac{1}{2}$-$\frac{i}{2}$ | D. | $\frac{1}{2}$+$\frac{i}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com